PgSQL · 源码分析 · PG优化器物理查询优化
Author: 康贤
在之前的一篇月报中,我们已经简单地分析过PG的优化器(PgSQL · 源码分析 · PG优化器浅析),着重分析了SQL逻辑优化,也就是尽量对SQL进行等价或者推倒变换,以达到更有效率的执行计划。本次月报将会深入分析PG优化器原理,着重物理查询优化,包括表的扫描方式选择、多表组合方式、多表组合顺序等。
表扫描方式
表扫描方式主要包含顺序扫描、索引扫描以及Tid扫描等方式,不同的扫描方式
- Seq scan,顺序扫描物理数据页
postgres=> explain select * from t1 ;
QUERY PLAN
-----------------------------------------------------
Seq Scan on t1 (cost=0.00..14.52 rows=952 width=8)
- Index scan,先通过索引值获得物理数据的位置,再到物理页读取
postgres=> explain select * from t1 where a1 = 10;
QUERY PLAN
--------------------------------------------------------------------
Index Scan using t1_a1_key on t1 (cost=0.28..8.29 rows=1 width=8)
Index Cond: (a1 = 10)
- Tid scan,通过page号和item号直接定位到物理数据
postgres=> explain select * from t1 where ctid='(1,10)';
QUERY PLAN
--------------------------------------------------
Tid Scan on t1 (cost=0.00..4.01 rows=1 width=8)
TID Cond: (ctid = '(1,10)'::tid)
选择度计算
- 全表扫描选择度计算
全表扫描时每条记录都会返回,所以选择度为1,所以rows=10000
EXPLAIN SELECT * FROM tenk1;
QUERY PLAN
-------------------------------------------------------------
Seq Scan on tenk1 (cost=0.00..458.00 rows=10000 width=244)
SELECT relpages, reltuples FROM pg_class WHERE relname = 'tenk1';
relpages | reltuples
----------+-----------
358 | 10000
- 整型大于或者小于选择度计算
EXPLAIN SELECT * FROM tenk1 WHERE unique1 < 1000;
QUERY PLAN
--------------------------------------------------------------------------------
Bitmap Heap Scan on tenk1 (cost=24.06..394.64 rows=1007 width=244)
Recheck Cond: (unique1 < 1000)
-> Bitmap Index Scan on tenk1_unique1 (cost=0.00..23.80 rows=1007 width=0)
Index Cond: (unique1 < 1000)
SELECT histogram_bounds FROM pg_stats
WHERE tablename='tenk1' AND attname='unique1';
histogram_bounds
------------------------------------------------------
{0,993,1997,3050,4040,5036,5957,7057,8029,9016,9995}
selectivity = (1 + (1000 - bucket[2].min)/(bucket[2].max - bucket[2].min))/num_buckets
= (1 + (1000 - 993)/(1997 - 993))/10
= 0.100697
rows = rel_cardinality * selectivity
= 10000 * 0.100697
= 1007 (rounding off)
- 字符串等值选择度计算
EXPLAIN SELECT * FROM tenk1 WHERE stringu1 = 'CRAAAA';
QUERY PLAN
----------------------------------------------------------
Seq Scan on tenk1 (cost=0.00..483.00 rows=30 width=244)
Filter: (stringu1 = 'CRAAAA'::name)
SELECT null_frac, n_distinct, most_common_vals, most_common_freqs FROM pg_stats
WHERE tablename='tenk1' AND attname='stringu1';
null_frac | 0
n_distinct | 676
most_common_vals|{EJAAAA,BBAAAA,CRAAAA,FCAAAA,FEAAAA,GSAAAA,JOAAAA,MCAAAA,NAAAAA,WGAAAA}
most_common_freqs | {0.00333333,0.003,0.003,0.003,0.003,0.003,0.003,0.003,0.003,0.003}
selectivity = mcf[3]
= 0.003
rows = 10000 * 0.003
= 30
备注:如果值不在most_common_vals里面,计算公式为:
selectivity = (1 - sum(mvf))/(num_distinct - num_mcv)
- cost计算
代价模型:总代价=CPU代价+IO代价+启动代价
postgres=> explain select * from t1 where a1 > 10;
QUERY PLAN
-----------------------------------------------------
Seq Scan on t1 (cost=0.00..16.90 rows=942 width=8)
Filter: (a1 > 10)
(2 rows)
其中:
postgres=> select relpages, reltuples from pg_class where relname = 't1';
relpages | reltuples
----------+-----------
5 | 952
(1 row)
cpu_operator_cost=0.0025
cpu_tuple_cost=0.01
seq_page_cost=1
random_page_cost=4
总cost = cpu_tuple_cost * 952 + seq_page_cost * 5 + cpu_operator_cost * 952 = 16.90 其他扫描方式cost计算可以参考如下函数:
postgres=> select amcostestimate,amname from pg_am ;
amcostestimate | amname
------------------+--------
btcostestimate | btree
hashcostestimate | hash
gistcostestimate | gist
gincostestimate | gin
spgcostestimate | spgist
(5 rows)
表组合方式
- Nest Loop
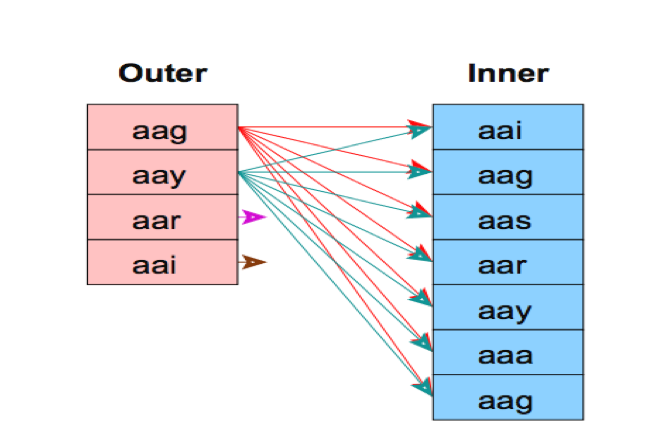
SELECT * FROM t1 L, t2 R WHERE L.id=R.id
假设:
M = 20000 pages in L, pL = 40 rows per page, N = 400 pages in R, pR = 20 rows per page.
select relpages, reltuples from pg_class where relname=‘t1’
L和R进行join
for l in L do
for r in R do
if rid == lid then ret += (r, s)
对于外表L每一个元组扫描内表R所有的元组
总IO代价: M + (pL * M) * N = 20000 + (4020000)400
= 320020000
- MergeJoin

主要分为3步:
(1) Sort L on lid 代价MlogM
(2) Sort R on rid 代价NlogN
(3) Merge the sorted L and R on lid and rid 代价M+N
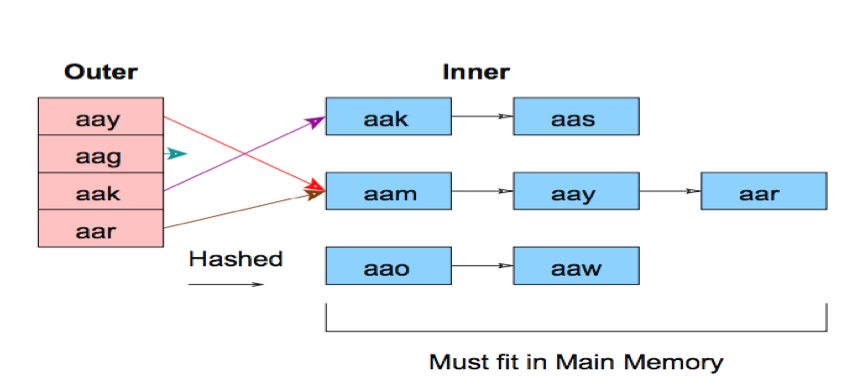
- HashJoin
使用HashJoin的前提是其中假设一个表可以完全放在内存中,实际过程中可能统计信息有偏差,优化器认为一个表可以放到内存中,事实上数据在内存中放不下,需要使用临时文件,这样会降低性能。
表的组合顺序
不同的组合顺序将会产生不同的代价,想要获得最佳的组合顺序,如果枚举所有组合顺序,那么将会有N!的排列组合,计算量对于优化器来说难以承受。PG优化器使用两种算法计算更优的组合顺序,动态规划和遗传算法。对于连接比较少的情况使用动态规划,否则使用遗传算法。
- 动态规划求解过程
PG优化器主要考虑将执行计划树生成以下三种形式:
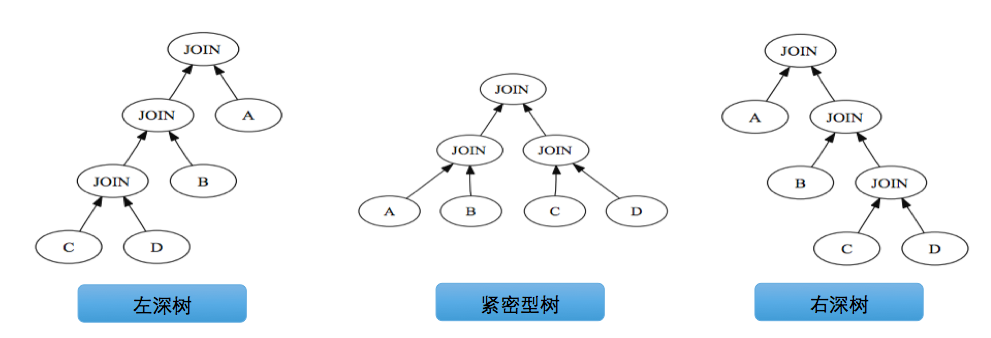
动态规划的思想可以参考百度百科动态规划,主要将待求解问题分解成若干个子问题,先求解子问题,然后从这些子问题的解得到原问题的解。具体应用在表组合顺序上,则是先考虑单表最优访问访问,然后考虑两种组合,再考虑多表组合,最终得到更优的解。
