PgSQL · 原理介绍 · PostgreSQL中的空闲空间管理
Author: haokang
背景
PostgreSQL的MVCC机制中,更新和删除操作并不是对原有的数据空间进行操作,而是通过对元组(tuple)的多版本形式来实现的。而由此引发了过期数据的问题,即当一个版本的元组对所有事物都不可见时,那么它就是过期的,此时它占用的空间是可以被释放的。
上述过期空间的释放工作是交给VACCUM来进行的。在这个过程中,VACCUM会将数据页上的过期元组的空间标记为可用,而当有新的数据插入时,也会优先使用这些可用空间。因此如何将这些可用空间管理起来,并在需要的时候能够高效地分配出去是一个需要解决的问题。
数据结构
PostgreSQL 8.4 引入了FSM(Free Space Map)结构来管理数据页中的空闲空间。FSM是存在以_fsm为后缀的文件中的,每个表都有一个对应的fsm文件。fsm文件的初始大小为24KB,在表创建以后的第一次VACCUM操作中被创建,而且在接下来的每次VACCUM操作中被更新。
$ll $PG_DATA/base/13878/
total 7824
-rw------- 1 postgres postgres 73728 Mar 19 19:26 1247
-rw------- 1 postgres postgres 24576 Mar 19 18:12 1247_fsm
FSM的存在的意义就是为了管理空闲资源,并且让它们可以快速地被再次使用,所以结构的设计要以小而快的目标。FSM的空间管理中,没有细粒度到数据页的每个比特,而是将最小单元定义为页大小(BLCKSZ)的256分之一,也就是说,在默认8KB数据页的大小下,从FSM的角度观察,它有256个单元。所以,为了表述这个256个单元的状态,FSM为每个数据页分配了一个字节的空间。这也是FSM在设计时,一个空间和时间的折中选择。
FSM页结构
为了可以快速去查找的需要的空间,FSM在对数据的组织上没有采用类似数组的线性数据结构,而是选择了树形结构来组织。在一般的空闲查询操作中,调用者想知道的就是当前能不能满足我的空闲需求,FSM中是将每个页的空余空间信息通过一个大根堆的形式组织的。在堆的结构下,调用者想要知道是否有满足需求的空间,只需要从堆的根获取到当前最大的空余空间就可以快速的判断,减少了整体的判断次数,提高效率。FSM页中堆的结构如下图所示:
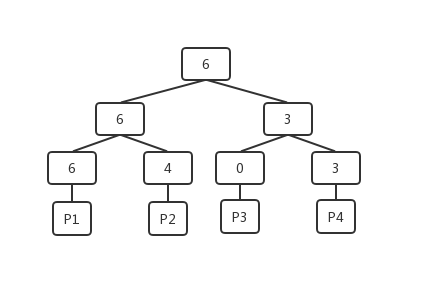
堆中的每个叶子节点都对应一个数据页,叶子节点上记录的是数据页的可用单元的个数,例如,上图中P1中当前包含了6个空闲单元。每个非叶子节点上的记录的则是它的子节点中较大的可用数目。实例的FSM页中,不一定是一个满二叉树的形式,在叶子节点的最右侧是可能存在空缺的,但是可以保证的是堆所需要的完全二叉树的组织方式,只要是叶子节点,都有相对应的数据页。
这样的结构提供了两个基本操作:更新和查找。我们以上面的图示为里介绍一下这两种操作:
- 当数据页P3的可用单元数量发生变化为5时(执行完VACCUM操作),先将它对应的叶子节点的记录由0更新为5,然后向上寻找父节点,父节点根据当前子节点的记录(5和3)选择较大的5更新为自己的记录,继续类似的操作递归更新直至根节点,这样的操作也是堆结构中一个典型的调整操作;
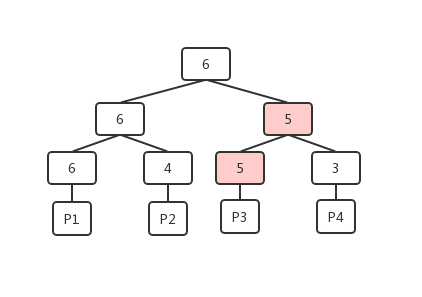
- 当调用方想要找到可以满足自己4个单元需求的数据页时,会先从FSM页的根开始进行比较,发现6大于自己的需求(如果不满足需求这时就可以返回了),则从子节点(6和3)中选择满足需求的左子节点,类似的比较递归向下,当出现两个子节点都可以满足需求的情况时,可以根据自身的策略来选择,以更接近需求的策略来选择的话,整个查找的过程如下图。
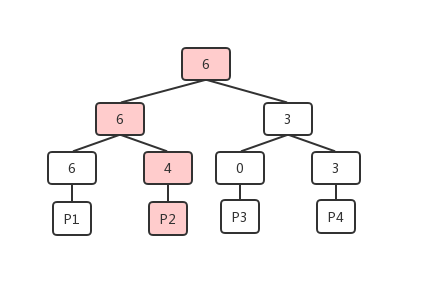
这样一个大根堆的结构,在实际存储的时候是以以为数组的形式保存的,利用完全二叉树中父子节点的关系来进行堆节点的访问。在如下图所示的数组中,每个元素对应堆中的一个节点。以某个非叶子节点为例,假设这个节点在数组中的序号为n,那么它的左子节点的序号则为n * 2,右子节点的序号则为n * 2 + 1;相反的,如果某个节点的序号为n,那么它的父节点的序号则为n / 2。
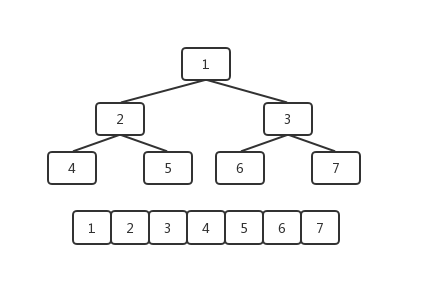
Higer-Level
为了把FSM页管理起来,FSM在不同的FSM页间页维护了一个类似的树形结构,PostgreSQL中称这种组织结构相较于FSM页来说是一种“Higher-level structure”。
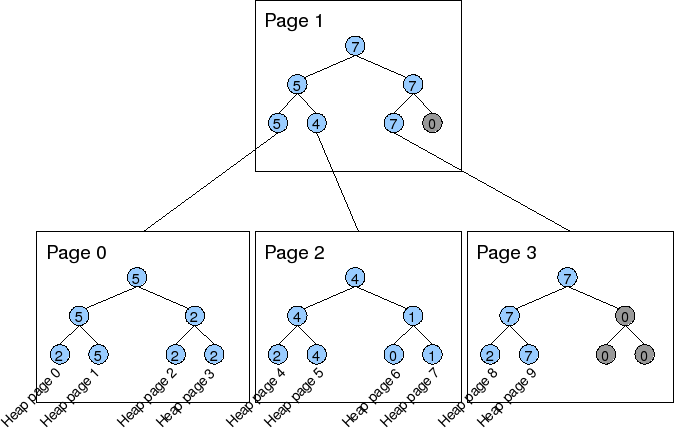
如上图所示,在Higher-Level的结构中,每个FSM页中的叶子节点对应的不仅是数据页,也可能是另外一个FSM页。当叶子节点对应的是FSM页时,逻辑是类似的,节点保存的是整个子FSM页中根节点的记录数(也就是该FSM中最大的可用单元数)。按照这样的关系,FSM页间组织不再是类似FSM页内的二叉树形式,而是多叉树。
一个FSM页大概可以存下(BLCKSZ - HeaderSize) / 2个数据页的可用空间信息,在默认8KB的页大小下,每个页大约可保存4000个数据页的信息。FSM页作为树形结构的节点,那么这个节点可以关联4000个子节点,以这样的规模扩展,只需要3层就可以管理其一个表的全部数据页。因为三层的FSM页可以管理的数据页数量约为4000^3,而PostgreSQL中每个表的数据页上限为2^32 - 1,4000^3 > 2^32。
在Higher-Level结构中定位一个数据页时需要用到三个概念:
- 层(level)
- 页序号(page number)
- 页槽(slot)
全部的叶子FSM页都在0层,它们的父FSM页在1层,根FSM页在2层。每层中FSM页的序号就是这个页在这一层的顺序位置。
实现分析
接下来,就从代码的角度来分析下FSM的定义和操作。
结构体
首先,先看一下FSM页的定义:
typedef struct
{
int fp_next_slot;
uint8 fp_nodes[FLEXIBLE_ARRAY_MEMBER];
} FSMPageData;
其中的fp_next_slot是指向了上次搜索到的slot的位置,接下来这个page的每次搜索都会从fp_next_slot标识的位置开始。这样的设定是为了:
- 可以使得不同的backend不至于同时在一个页中搜索导致争抢;
- 在多个backend的访问时可以给与多个请求一个尽可能连续的内存空间,这样也有利于操作系统去进行预取(prefetch)和批量写。
fp_node则是存储当前FSM也中的堆结构,因为是完全二叉树的形式,所以是可以按层遍历依次放入到一维数组中的,这样也可以通过父子节点的下表关系方便的在堆中进行移动。
可用页查找操作
接下来就是常用的两个操作:查找和更新。FSM页的查找操作对应的是fsm_search_avail函数,它的逻辑如下:
int
fsm_search_avail(Buffer buf, uint8 minvalue, bool advancenext,
bool exclusive_lock_held)
...
if (fsmpage->fp_nodes[0] < minvalue) // 如果堆根不满足要求,那么不用继续查找了
return -1;
target = fsmpage->fp_next_slot; // 从上次查找到的slot开始查找
if (target < 0 || target >= LeafNodesPerPage)
target = 0;
target += NonLeafNodesPerPage;
nodeno = target;
while (nodeno > 0)
{
if (fsmpage->fp_nodes[nodeno] >= minvalue) //如果找到满足要求的节点,则跳出
break;
nodeno = parentof(rightneighbor(nodeno)); // 否则尝试去它的父节点寻找
}
// 从找到的非叶子节点开始向下去找满足空间的叶子节点
while (nodeno < NonLeafNodesPerPage)
{
int childnodeno = leftchild(nodeno);
if (childnodeno < NodesPerPage &&
fsmpage->fp_nodes[childnodeno] >= minvalue) // 如果左子节点满足,则从左子节点继续向下找
{
nodeno = childnodeno;
continue;
}
childnodeno++; /* point to right child */
if (childnodeno < NodesPerPage &&
fsmpage->fp_nodes[childnodeno] >= minvalue) // 否则,如果右子节点满足,则从右子节点向下
{
nodeno = childnodeno;
}
else // 如果父节点满足,但孩子节点都不满足,则需要更新将FSM锁定,然后重新从叶子节点开始更新整个堆
{
RelFileNode rnode;
ForkNumber forknum;
BlockNumber blknum;
BufferGetTag(buf, &rnode, &forknum, &blknum);
if (!exclusive_lock_held) // 尝试锁定当前FSM页
{
LockBuffer(buf, BUFFER_LOCK_UNLOCK);
LockBuffer(buf, BUFFER_LOCK_EXCLUSIVE);
exclusive_lock_held = true;
}
fsm_rebuild_page(page); // 重建页结构
MarkBufferDirtyHint(buf, false);
goto restart;
}
}
fsmpage->fp_next_slot = slot + (advancenext ? 1 : 0);
return slot;
}
上面就是在一个FSM页中的查找过程:
- 如果根节点的记录不满足要求,那么不用继续查找了,当前页上没有满足要求的slot;
- 查找的起点是上次找到满足要求的page对应的slot;
- 然后从当前slot开始向上寻找,直到有节点的空闲资源满足要求,如果没有满足要求的节点,最终会找到根节点;
- 从当前的非叶子节点开始向下找:
- 如果左子节点满足则从左侧向下寻找;
- 如果右子节点满足,则从右侧向下寻找;
- 否则,说明父节点的记录和孩子节点的记录不匹配,需要锁定当前FSM页,重新更新堆结构,然后从第一步开始重试;
- 找到之后,将当前FSM的
fp_next_slot更新。
上面介绍的是,在FSM页内的查找过程,Higher Level的超找逻辑,在fsm_search()中,如下:
static BlockNumber
fsm_search(Relation rel, uint8 min_cat)
{
int restarts = 0;
FSMAddress addr = FSM_ROOT_ADDRESS; // 从根页开始查找
for (;;)
{
...
if (BufferIsValid(buf))
{
LockBuffer(buf, BUFFER_LOCK_SHARE);
slot = fsm_search_avail(buf, min_cat,
(addr.level == FSM_BOTTOM_LEVEL),
false); // 在当前FSM页中查找可用空间
if (slot == -1)
max_avail = fsm_get_max_avail(BufferGetPage(buf));
UnlockReleaseBuffer(buf);
}
else
slot = -1;
if (slot != -1)
{
if (addr.level == FSM_BOTTOM_LEVEL) // 如果已经查找到第0层,则返回找到的数据页信息
return fsm_get_heap_blk(addr, slot);
addr = fsm_get_child(addr, slot); // 否则,继续向下寻找
}
else if (addr.level == FSM_ROOT_LEVEL) // 如果在第二层页没有满足要求,则找不到满足要求的数据页
{
return InvalidBlockNumber;
}
...
}
}
在FSM页间的查找和页内的查找逻辑是类似的,只不过将其放大到了页间的逻辑中,步骤如下:
- 从第2层的根页开始查找;
- 若当前页找到满足要求的slot:
- 如果当前是最底层,第0层,那么找到的slot可以转换为数据页的信息输出,查找结束;
- 否则,继续向下寻找;
- 若当前页没有找到满足要求的slot:
- 如果当前页是最顶层,则说明现在没有满足需求的数据页,返回;
- 如果不是,则说明父页的记录和子页不一致,尝试修复,然后重试查找;
结构恢复
从上面的查找逻辑中可以看到,不论是页内还是页间都可能出现父子节点(或页)的记录不一致的情况:
- 在FSM页内,可能由于系统Crash,导致FSM页在只有部分数据被更新到磁盘的情况下,会出现不一致;
- 在FSM页间,可能由于子页出现的更新还反馈更新到父页导致。
不论是哪种情况,都可以通过从底层数据重新向上更新的办法来修复。另外,定期的VACCUM操作也会更新最低层的记录,同时触发向上的更新,也是一种定期修复FSM的方式。FSM对准确度的要求并不高,它可以尽量尝试维护一个最新的可用空间的记录,但不保证它当前的记录一定是完全准确的,但是在运行中会有多种方式来不断的修复结构本身。