MySQL · 源码解析 · MySQL 8.0.23 Hypergraph Join Optimizer代码详解
Author: 道客
MySQL JOIN简介
MySQL本身没有常规意义上的执行计划,一般情况就是通过JOIN和QEP_TAB这两个结构组成。QEP_TAB 的全称是Query Execution Plan Table,这个“Table“可以是物理表、内存表、常量表、子查询的结果表等等。作为整个单独JOIN执行计划载体之前还承担着整个执行路径的调用和流转,但是从8.0.20后,全面的生成了独立的Iterator执行器引擎模式。在8.0.22中,又引入了AccessPath概念,真正的生成了独立的执行计划,从而进一步做到了优化过程到树型执行计划,最后到Iterator载体在执行引擎中的执行。
MySQL原始的Join都是依赖于QEP_TAB列表,因为原来MySQL并不支持其他形态的Join结构,只支持左深树,那很容易直接使用数组来表示就可以了。优化器在生成执行计划只需要在QEP_TAB上增加JOIN的属性op_type,就可以递归去使用不同的Join方法和表访问方式了。
// Operation between the previous QEP_TAB and this one.
enum enum_op_type {
// Regular nested loop.
OT_NONE,
// Aggregate (GROUP BY).
OT_AGGREGATE,
// Various temporary table operations, used at the end of the join.
OT_MATERIALIZE,
OT_AGGREGATE_THEN_MATERIALIZE,
OT_AGGREGATE_INTO_TMP_TABLE,
OT_WINDOWING_FUNCTION,
// Block-nested loop (rewritten to hash join).
OT_BNL,
// Batch key access.
OT_BKA
} op_type = OT_NONE;
Hypergraph Join Optimizer
官方共分了11个Patch来提交对于Join优化器的增强,当然其中包含了对优化器和执行器分离更进一步重构,我们先来看看官方是怎么提交这样的重大重构的。
[Basic] 动态规划查询超图算法(DPhyp-Hypergraph partitioning algorithm) 官方首先实现了基于DPhyp的动态规划查询超图算法,论文可以搜索《Dynamic Programming Strikes Back》。数据库中关于Join ordering算法有很多,引用2,3中的作者已经做了详尽的解释。我这里只做简单的介绍。
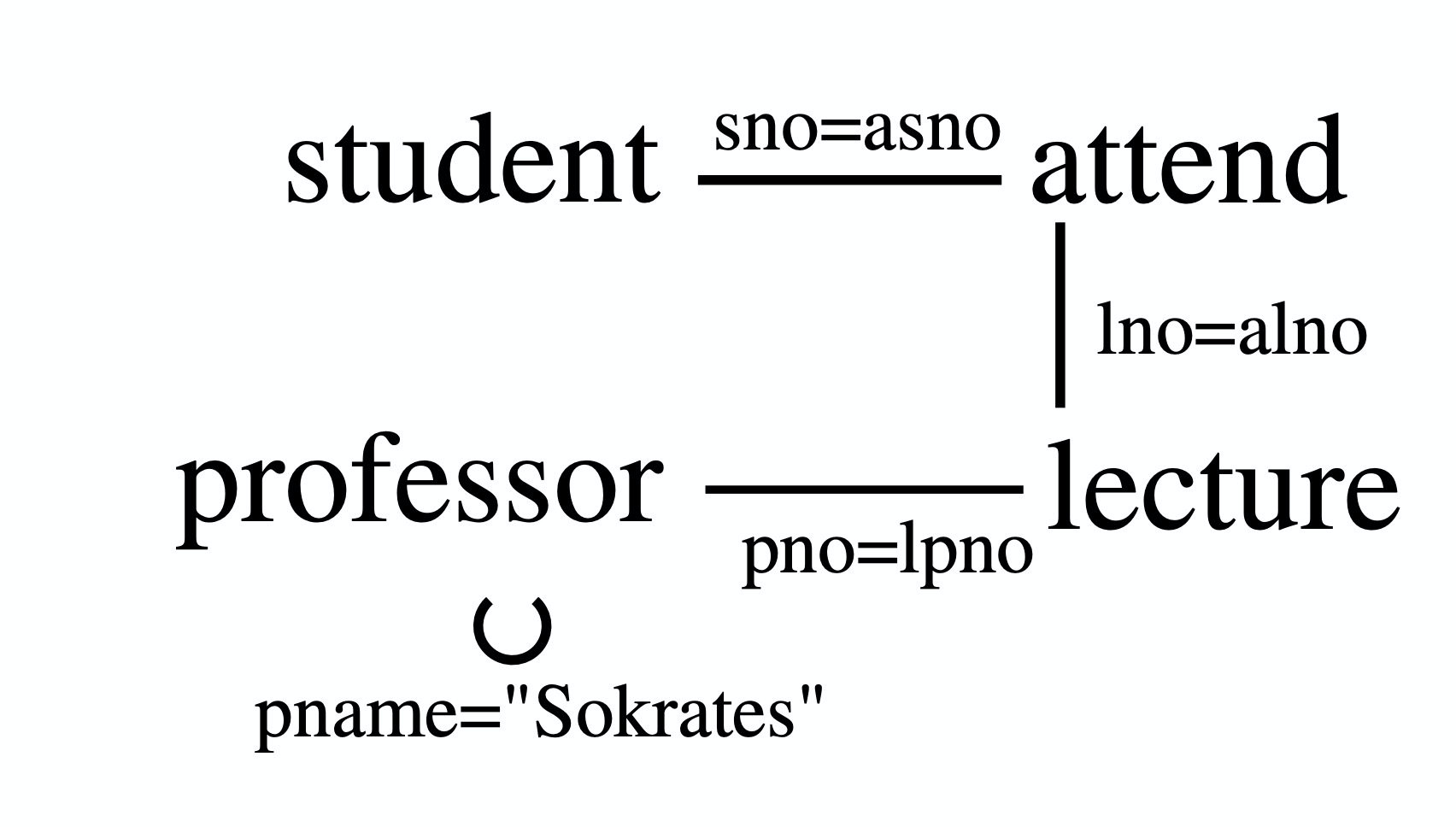
每一个Query,都可以定义为一个无向Query Graph,包括查询中的所有关系R1,R2,…,Rn作为节点;连接谓词表达式作为边,如a1 = a2 (a1 ∈ Ri,a2 ∈ Rj);连接谓词中包含常量会形成自边(self-edge),如a1 = const (a1 ∈ Ri);大部分的自边在Join算法里是不考虑的,因为它会被下推下图。例如对于 select * from Student s, Attend a, Lecture l, Professor p where s.sno = a.asno and a.alno = l.lno and l.lpno = p.pno and p.pname = ‘Larson’,有如下Query Graph结构:
对于Join Tree,一般会有以下几种:left-deep tree、right-deep tree、zigzag tree和bushy tree。前三种是属于线性Join tree。MySQL之前采取左深树,为了考虑更好的支持Hash Join和NestLoop Join的选择,现在开始考虑Bushy Tree了。为了避免任何时候的笛卡尔积Join,线性Join的Join ordering算法通常很简单。那么为什么要引入复杂的Bushy Tree。假设定义Query(R1, R2, R3)有如下属性,y |R1| = 10, |R2| = 20, |R3| = 20, |R4| = 10, f1,2 = 0.01, f2,3 = 0.5, f3,4 = 0.01。||代表行数,fn,m代表Rn和Rm的选择率,可以看到Bushy Tree有更好的执行效率。

不过遗憾的是,Bushy Tree的搜索可能性非常大:
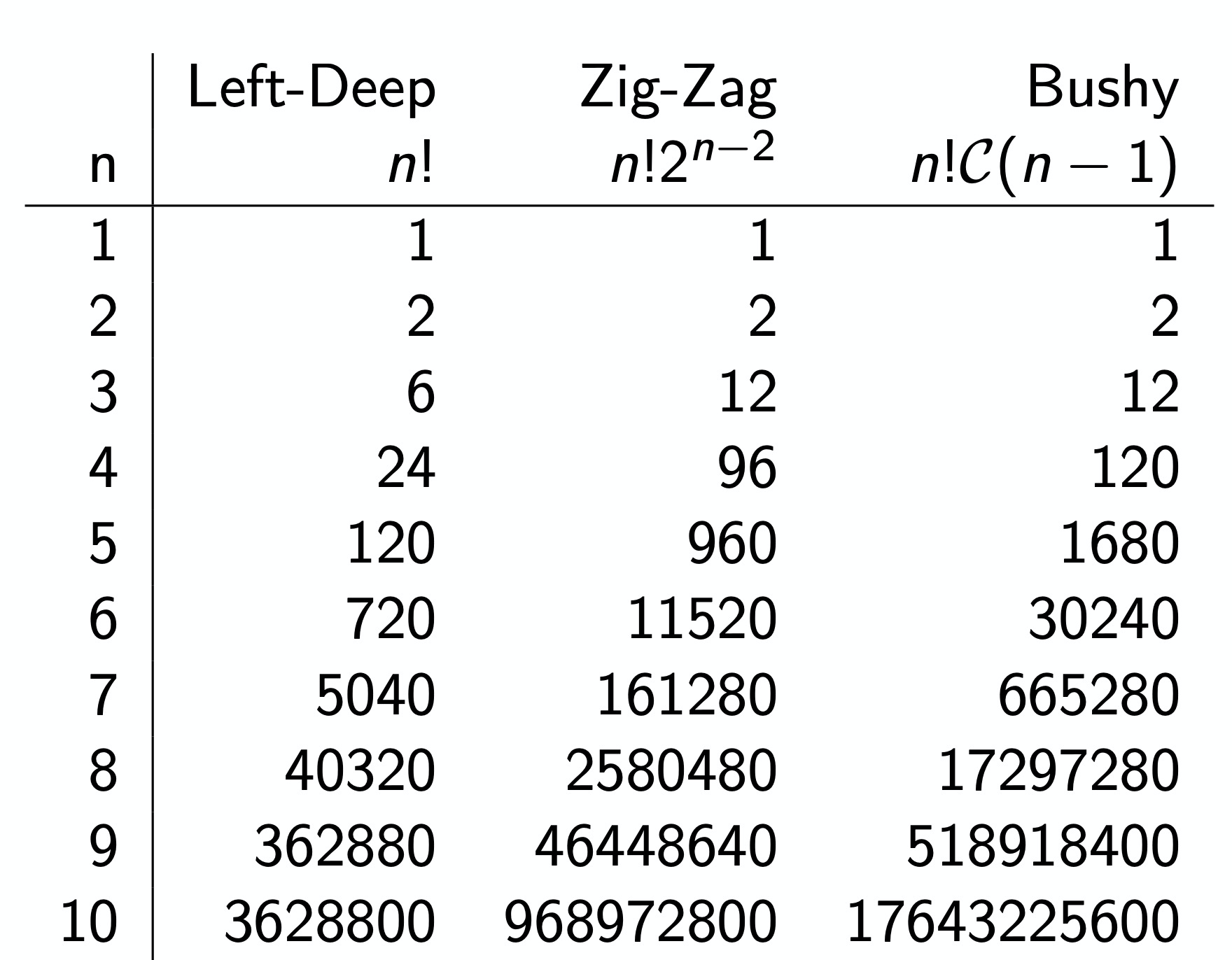
因此,原始左深树使用的Greedy Heuristics算法,在Bushy Tree下,计算Join Ordering通常使用动态规划算法(DPccp和DPhyp)。
DPccp的算法如下:

但是DPccp有很多限制:复杂谓词,涉及到多个表(R1,R2,R3)做为连接,例如:R1.a + R2.b + R3.c = R4.d + R5.e + R6.f ;只支持inner joins;因此引入了新的基于Hypergraph的算法DPhyp。
select *
from R1 r1, R2 r2, R3 r3,
R4 r4, R5 r5, R6 r6
where r1.a=r2.a and r2.b=r3.c and
r4.d=r5.d and r5.e=r6.e and
abs(r1.f + r3.f )
= abs(r4.g + r6.g)
介绍算法先介绍下基本概念超图(hypergraph)相比普通的图,其特点是图中的节点是一个集合,称为超节点(hypernode),图中的边所连接的是超节点,即连接两个集合。这类边称为超边(hyperedge)。超图就是由超节点和超边作为最基本元素而构成的。有了超图那么上面的Join Graph可以变成:
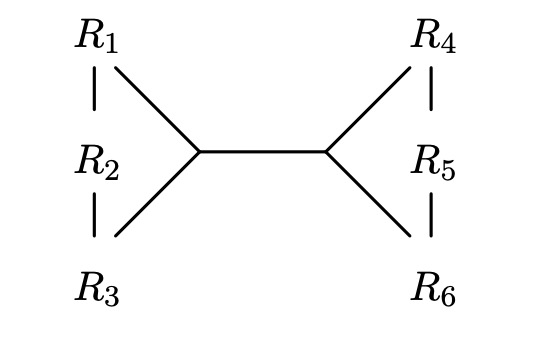
由于使用DPccp和Top-Down Partition Search,不能够解决outer join,antijoin的不能自由重排的算法。
MySQL目前采用Bitmap(64bit)来表示,假设Join table个数不会超过61个,看下它的定义
+struct Hyperedge {
+ // The endpoints (hypernodes) of this hyperedge. See the comment about
+ // duplicated edges in Node.
+ //
+ // left and right may not overlap, and both must have at least one bit set.
+ NodeMap left;
+ NodeMap right;
+};
+
+struct Hypergraph {
+ std::vector<Node> nodes; // Maximum 8*sizeof(NodeMap) elements.
+ std::vector<Hyperedge> edges;
+
+ void AddNode();
+ void AddEdge(NodeMap left, NodeMap right);
+};
基本算法流程如下:
- 找到一个图中种子节点Ri
- 不断增加i去找hyperedges,不考虑不连接的和已经处理过的。
- 对于每一个连通子图subgraph (csg),再重复1和2步骤,找出一个仍然可以连通子图(complement, cmp),然后连接这个图的cmp成为更大的连通子图(csg-cmp-pair).
- 当找到一个csg-cmp-pair,就形成一个可以进行估算的subjoin。
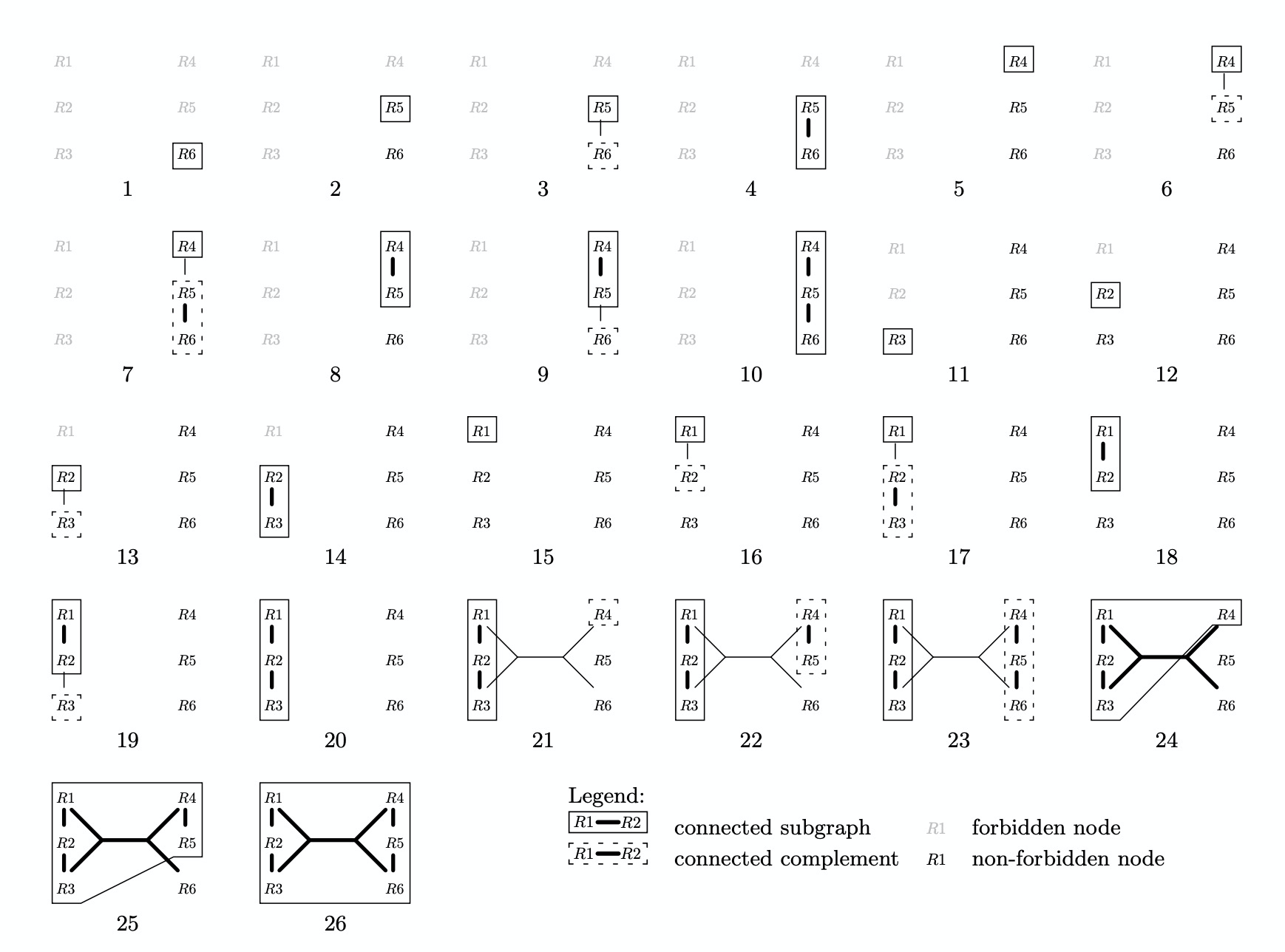
感兴趣可以阅读相应的论文和MySQL的代码(sql/join_optimizer)。
QEP_TAB和执行器Iterator解藕,重新来设置InnoDB row buffer
众所周知,QEB_TAB结构上承载了很多信息,除了上面表访问和Join方法的信息之外,还有InnoDB row buffer、表访问的优化访问方式(ref/range/loose scan/first match/materialize)、附加属性(having/distinct/sort/icp/lateral derived/mrr/cte)、基本物理表结构TABLE_LIST等。作为删除QEP_TAB的基础,首先先做了和执行器的解藕工作,Iterator和QEP_TAB分离。
class TableScanIterator final : public TableRowIterator {
public:
- // Accepts nullptr for qep_tab; qep_tab is used only for setting up record
- // buffers.
- //
- // The pushed condition can be nullptr.
+ // “expected_rows” is used for scaling the record buffer.
+ // If zero or less, no record buffer will be set up.
//
// "examined_rows", if not nullptr, is incremented for each successful Read().
- TableScanIterator(THD *thd, TABLE *table, QEP_TAB *qep_tab,
+ TableScanIterator(THD *thd, TABLE *table, double expected_rows,
ha_rows *examined_rows);
接下来解藕
-static bool init_index_and_record_buffer(const QEP_TAB *qep_tab, handler *file,
+static bool init_index(TABLE *table, handler *file, uint idx, bool sorted) {
-bool set_record_buffer(const QEP_TAB *tab);
+bool set_record_buffer(TABLE *table, double expected_rows_to_fetch);
=>
- return init_index_and_record_buffer(m_qep_tab, m_qep_tab->table()->file,
- m_ref->key, m_use_order);
+ if (table()->file->inited) return false;
+ if (init_index(table(), table()->file, m_ref->key, m_use_order)) {
+ return true;
+ }
+ return set_record_buffer(table(), m_expected_rows);
实现CostingReceiver和转化查询块select_lex成为超图hypergraph
MySQL 8.0.23提供了支持hypergraph的优化器模型的第一个原型版本,通过set optimizer_switch=”hypergraph_optimizer=on”;来打开,主要和原有的优化器区别在于:
- 不再局限于左深树的执行计划
- 用DPhyp动态规划算法代替了强力算和启发式的剪枝方式,减少了搜索空间,当然还有一些限制
- Hash join成为主要的选择方式
- 直接和AccessPath互通,而非直接生成Iterators
主要通过FindBestQueryPlan函数来实现,逻辑如下:
- 先判断是否属于新优化器可以支持的Query语法(CheckSupportedQuery),不支持的直接返回错误ER_HYPERGRAPH_NOT_SUPPORTED_YET
- 转化top_join_list变成JoinHypergraph结构。由于Hypergraph是比较独立的算法层面的实现,JoinHypergraph结构用来更好的把数据库的结构包装到Hypergraph的edges和nodes的概念上的。
- 通过EnumerateAllConnectedPartitions实现论文中的DPhyp算法
- CostingReceiver类包含了过去JOIN planning的主要逻辑,包括根据cost选择相应的访问路径,根据DPhyp生成的子计划进行评估,保留cost最小的子计划。
- 得到root_path后,接下来处理group/agg/having/sort/limit的。对于Group by操作,目前Hypergraph使用sorting first + streaming aggregation的方式。
FindBestQueryPlan最终返回确定的执行计划root_path后,通过CreateIteratorFromAccessPath函数生成对应的执行Iterator树,在Iterator执行器中执行。
举例说明:
两个连通子图
root:test> explain format=tree select * from t1,t2,t3,t4 where t2.f2 = t1.a and t1.a = t3.a;
+------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------+
| EXPLAIN |
+------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------+
| -> Hash cartesian product (no condition) (cost=1.83 rows=2)
-> Inner hash join (t2.f2 = t1.a) (cost=1.55 rows=2)
-> Table scan on t2 (cost=0.25 rows=2)
-> Hash
-> Inner hash join (t1.a = t3.a) (cost=1.27 rows=1)
-> Table scan on t1 (cost=1.00 rows=1)
-> Hash
-> Table scan on t3 (cost=0.25 rows=1)
-> Hash
-> Table scan on t4 (cost=0.25 rows=1)
|
一个连通子图
root:test> explain format=tree select * from t1,t2,t3,t4 where t2.f2 = t1.a and t1.a = t3.a and t2.f2 = t4.pk and t1.a = t4.pk;
+----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------+
| EXPLAIN |
+----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------+
| -> Inner hash join (t2.f2 = t4.pk), (t1.a = t4.pk) (cost=1.83 rows=2)
-> Inner hash join (t2.f2 = t1.a) (cost=1.55 rows=2)
-> Table scan on t2 (cost=0.25 rows=2)
-> Hash
-> Inner hash join (t1.a = t3.a) (cost=1.27 rows=1)
-> Table scan on t1 (cost=1.00 rows=1)
-> Hash
-> Table scan on t3 (cost=0.25 rows=1)
-> Hash
-> Table scan on t4 (cost=0.25 rows=1)
|
通过打开opt_trace来看下整个过程
{
"steps": [
{
"join_preparation": {
"select#": 1,
"steps": [
{
"expanded_query": "/* select#1 */ select `t1`.`a` AS `a`,`t2`.`f2` AS `f2`,`t3`.`a` AS `a`,`t3`.`b` AS `b`,`t4`.`pk` AS `pk`,`t4`.`col_int_nokey` AS `col_int_nokey`,`t4`.`col_int_key` AS `col_int_key`,`t4`.`col_varchar_nokey` AS `col_varchar_nokey` from `t1` join `t2` join `t3` join `t4` where ((`t2`.`f2` = `t1`.`a`) and (`t2`.`f2` = `t4`.`col_int_key`))"
}
]
}
},
{
"join_optimization": {
"select#": 1,
"steps": [
{
"condition_processing": {
"condition": "WHERE",
"original_condition": "((`t2`.`f2` = `t1`.`a`) and (`t2`.`f2` = `t4`.`col_int_key`))",
"steps": [
{
"transformation": "equality_propagation",
"resulting_condition": "((`t2`.`f2` = `t1`.`a`) and (`t2`.`f2` = `t4`.`col_int_key`))"
},
{
"transformation": "trivial_condition_removal",
"resulting_condition": "((`t2`.`f2` = `t1`.`a`) and (`t2`.`f2` = `t4`.`col_int_key`))"
}
]
}
},
{
"substitute_generated_columns": {
}
},
{
"join_optimizer": [
"Join list after simplification:",
"* t4 join_type=inner",
"* t3 join_type=inner",
"* t2 join_type=inner",
"* t1 join_type=inner",
"",
"Made this relational tree; WHERE condition is ((t2.f2 = t1.a) and (t2.f2 = t4.col_int_key)):",
"* Inner join (no join conditions)",
" * Inner join (no join conditions)",
" * Inner join (no join conditions)",
" * t1",
" * t2",
" * t3",
" * t4",
"",
"After pushdown; remaining WHERE conditions are (none):",
"* Inner join (equijoin condition = (t2.f2 = t4.col_int_key))",
" * Cartesian product",
" * Inner join (equijoin condition = (t2.f2 = t1.a))",
" * t1",
" * t2",
" * t3",
" * t4",
"",
"Selectivity of join (t2.f2 = t1.a):",
" - found an index in t1.a for (t2.f2 = t1.a), selectivity = 1.000",
"Selectivity of join [cartesian product]:",
"Selectivity of join (t2.f2 = t4.col_int_key):",
" - found an index in t4.col_int_key for (t2.f2 = t4.col_int_key), selectivity = 1.000",
"",
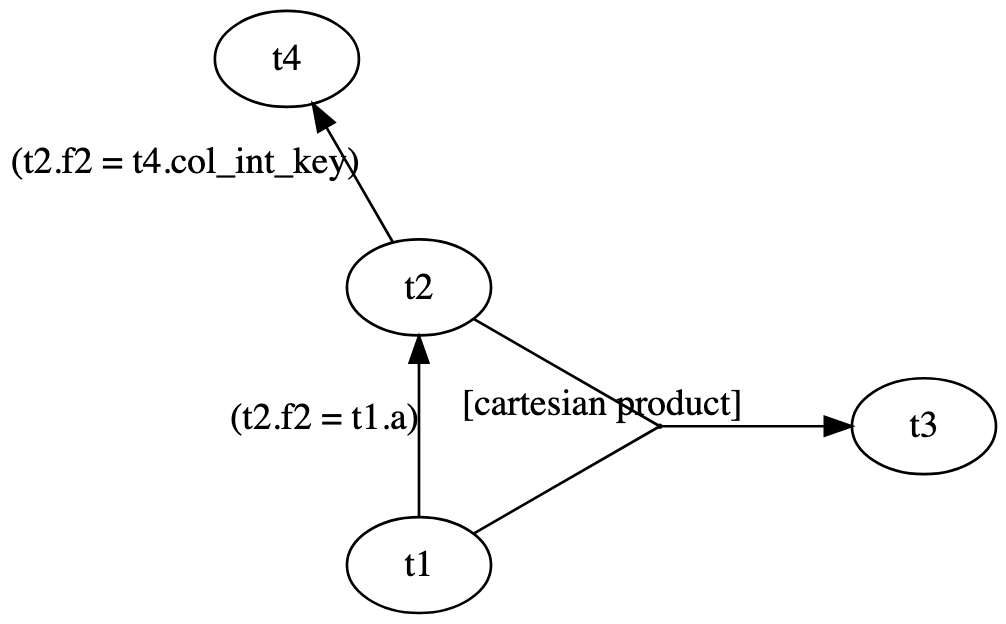
"Constructed hypergraph:",
"digraph G { # 3 edges",
" t1 -> t2 [label=\"(t2.f2 = t1.a)\"]",
" e2 [shape=circle,width=.001,height=.001,label=\"\"]",
" t1 -> e2 [arrowhead=none,label=\"\"]",
" t2 -> e2 [arrowhead=none,label=\"\"]",
" e2 -> t3 [label=\"[cartesian product]\"]",
" t2 -> t4 [label=\"(t2.f2 = t4.col_int_key)\"]",
"}",
"",
"Enumerating subplans:",
"Found node t4 [rows=1, cost=0.2]",
"Found node t3 [rows=1, cost=0.2]",
"Found node t2 [rows=2, cost=0.2]",
"Found sets {t2} and {t4}, connected by condition (t2.f2 = t4.col_int_key) [rows=2, cost=0.5]",
" - first alternative for this join, keeping",
"Found node t1 [rows=1, cost=1.0]",
"Found sets {t2} and {t1}, connected by condition (t2.f2 = t1.a) [rows=2, cost=1.3]",
" - first alternative for this join, keeping",
"Found sets {t2,t4} and {t1}, connected by condition (t2.f2 = t1.a) [rows=2, cost=1.6]",
" - first alternative for this join, keeping",
"Found sets {t1,t2} and {t4}, connected by condition (t2.f2 = t4.col_int_key) [rows=2, cost=1.6]",
" - more expensive than old cost 1.6, discarding",
"Found sets {t1,t2} and {t3}, connected by condition [cartesian product] [rows=2, cost=1.6]",
" - first alternative for this join, keeping",
"Found sets {t1,t2,t3} and {t4}, connected by condition (t2.f2 = t4.col_int_key) [rows=2, cost=1.8]",
" - first alternative for this join, keeping",
"Found sets {t1,t2,t4} and {t3}, connected by condition [cartesian product] [rows=2, cost=1.8]",
" - more expensive than old cost 1.8, discarding",
"",
"Enumerated 9 subplans."
]
}
]
}
}
]
}
可以看到官方MySQL还提供了查看Graph图的Json格式可视化脚本,我们可以通过online graph看到连通图: