PolarDB对ordering index代价计算的改进
Author: 郑博(映尧)
前言
ordering index选错是线上经常遇到的一种慢查。典型的例子是:
背景:time 与 id 有很强的关联
例一: select * from t where time > (CURDATE() - INTERVAL 7 DAY) order by id limit 2;
例二: select * from t where time > (CURDATE() - INTERVAL 7 DAY) order by id desc limit 2;
对于例一,如果选中了ordering index,那么几乎要访问完整张表的数据,才能找到最近七天的数据。使用idx_time作range访问是最佳的。
对于例二,使用ordering index倒序扫描,能够立即找到满足条件的数据。但是使用time的range条件就要访问更多的数据。使用idx_id的ordering访问是最佳的。
慢查出现的原因在于ordering index访问代价的计算公式相对粗糙,对于这里的例1和例2,ordering index的实际访问耗时天差地别,但其估算的ordering index访问代价相近。
Ordering index代价的原生算法
mysql原生的ordering index代价计算有一个基本的前提假设:符合where条件的数据行在ordering index上均匀分布。
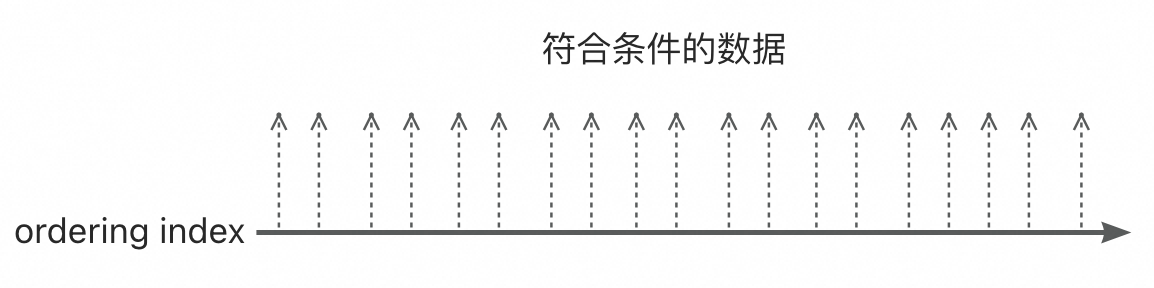
具体的代价公式为:

这里refkey_rows_estimate表示此表的最佳访问方式(除ordering index外)的访问行数。
因此,原始的计算方式存在两点缺陷:
- 符合过滤条件的数据在ordering index上分布可能不均匀。
- 使用最佳访问索引的访问行数估算,代替符合过滤条件的行数,忽略了不在此索引上的条件的过滤性。
本文针对第一点缺陷作分析,并提出相应的优化方案。
例1和例2的ordering index代价估算错误也完全是由缺陷1导致的。
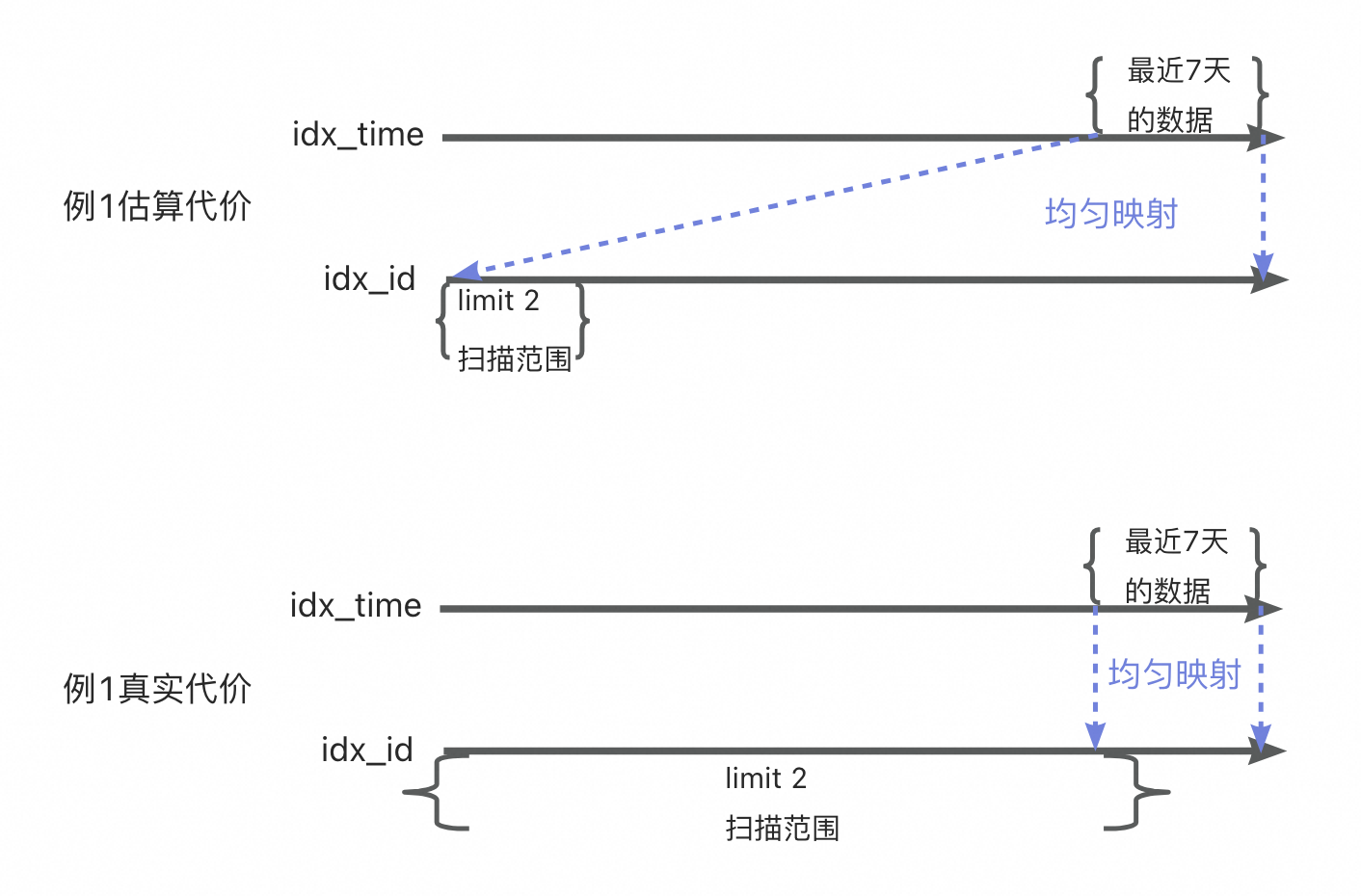
考虑数据相关性的新算法
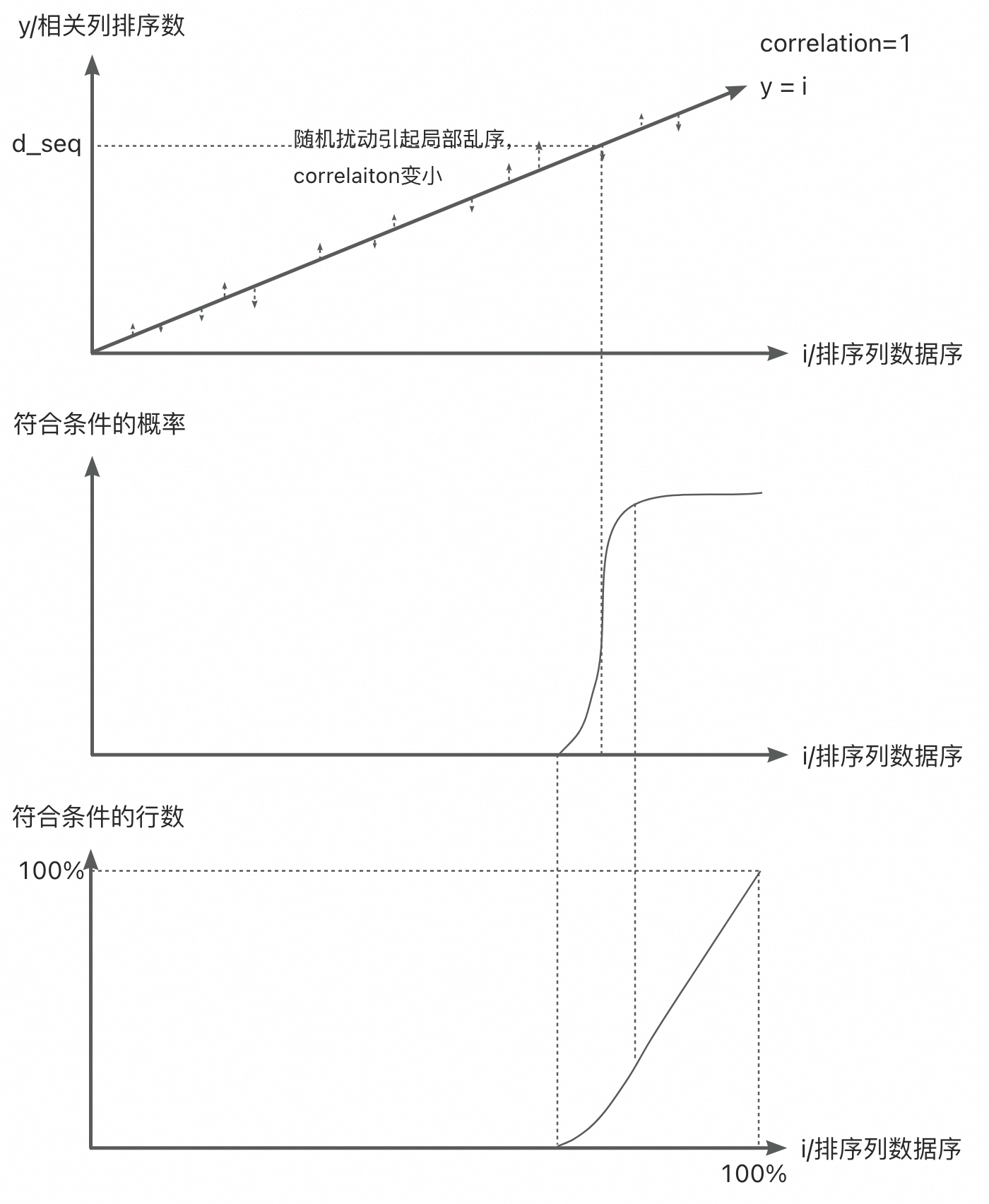
原始算法认为,在ordering index从左往右扫描的过程当中,符合条件的数据均匀分布。
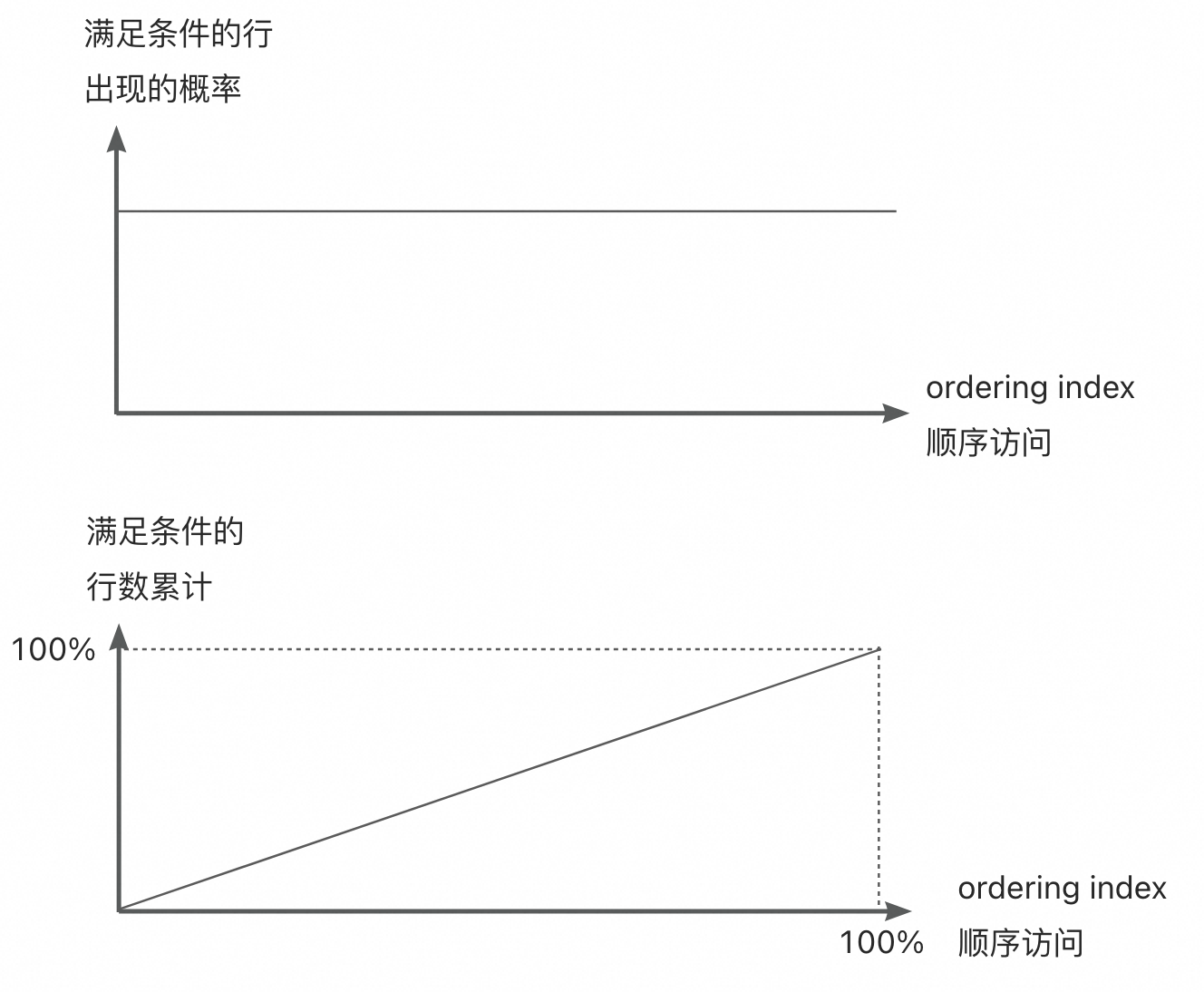
例1的代价估算图已经指出,问题的根源在于数据分布和数据相关性。由于time列和id列强正相关,最近七天的数据所对应的id一定是很大的,对应于idx_id索引的右边界附近的一小段。从左往右扫描的过程当中,符合条件的数据分布非常不均匀。
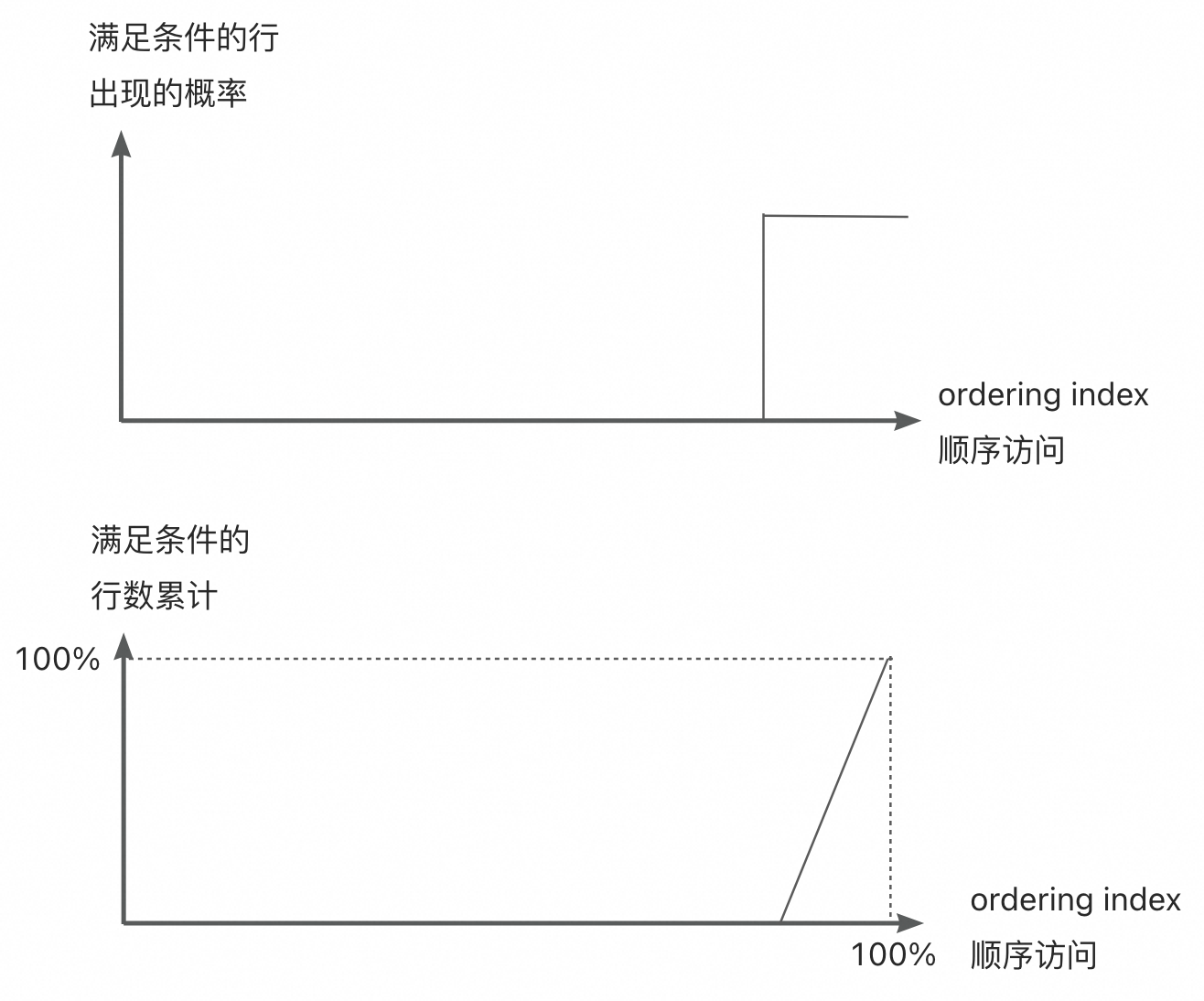
如果,我们能够获知ordering index扫描过程中,符合条件的数据分布,那计算精准的扫描行数就是可能的。在correlation=1的情况下,id列和time列完全正相关,符合条件的数据分布完全由上图描述。
当correlation != 1.0,但是接近1.0,某一行数据的id序与time序总体上正相关,局部存在乱序:
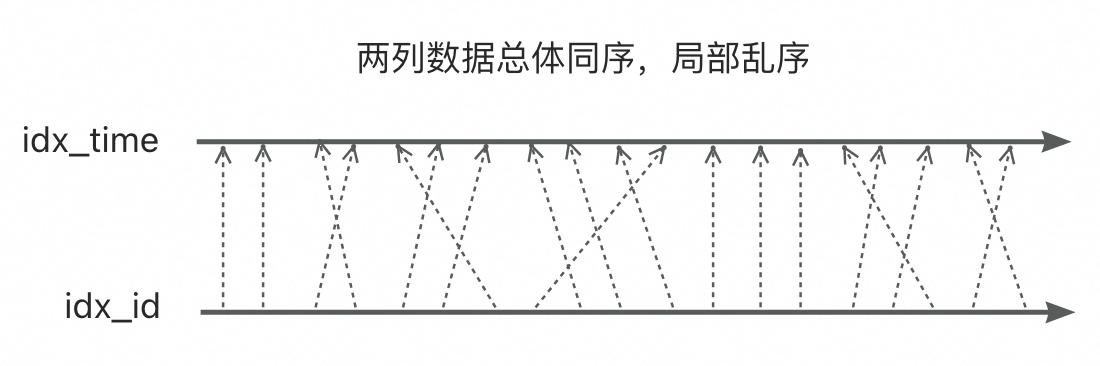
id和time之间的correlation不足以直接推演出这两列之间完整的映射关系。但是,如果对time列和id列的数据分布关联作特定的假设,我们可以从correlation反推特定假设下的数据关联,还原数据分布,计算预期扫描行数。这种做法还原的数据关联可能与真实分布不匹配,但总会比无关假设要强很多,且在correlation约等于1的情况下,与真实情况不会偏差太大。
关联数据的分布假设
假设: correlation约等于1的情况是,correlation=1情况的随机扰动。
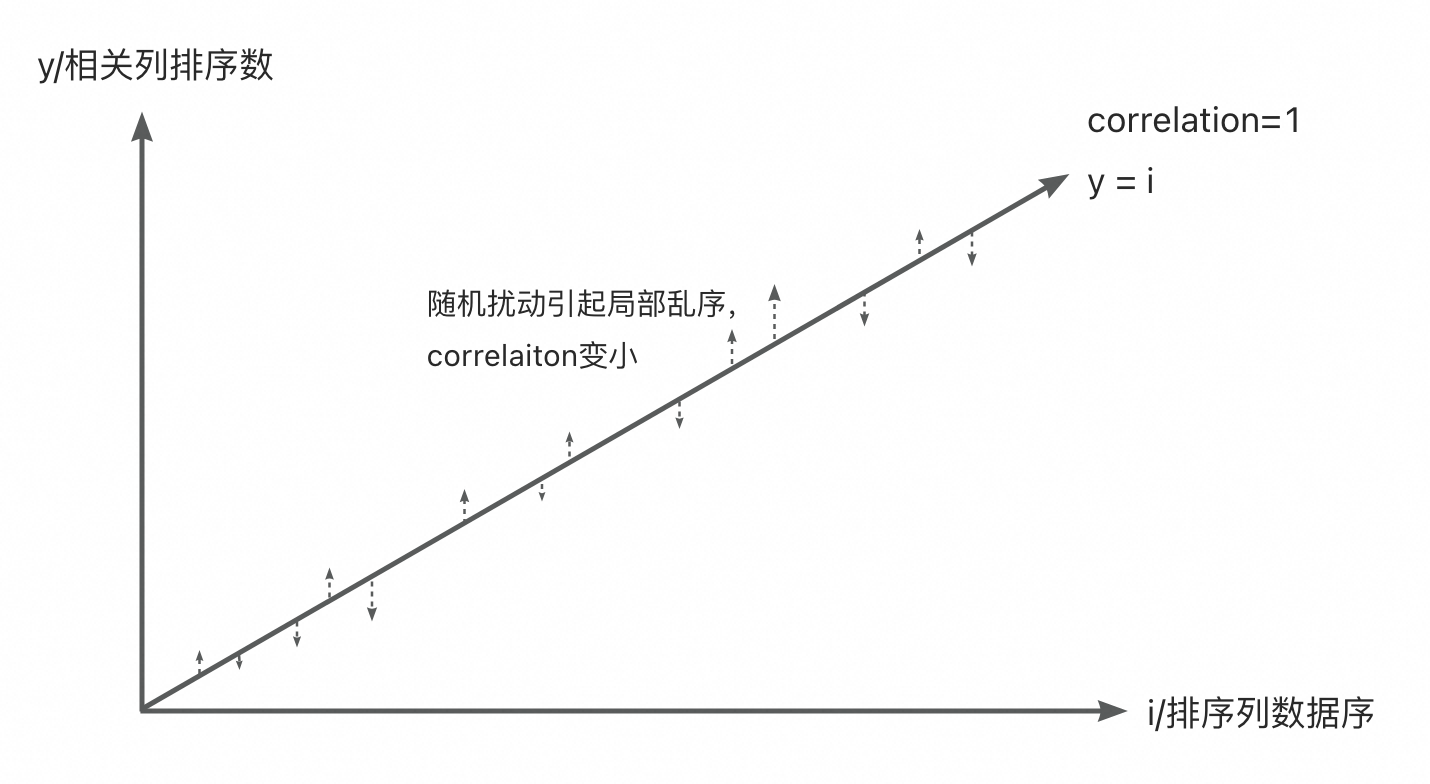
即在correlation 约等于 1 的情况下的数据序为:
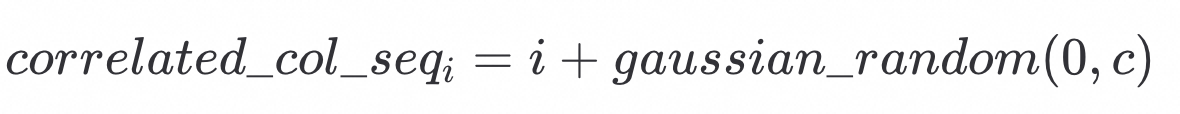
这种假设可能会突破排序边界0和n,但是只考虑c较小的情况,这个假设有其合理性。
求解预期扫描行
对于i = 0 ~ k的扫描, 满足
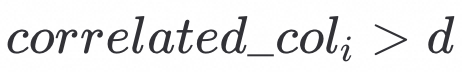 的数据行数:
的数据行数:

其数学期望为:

其中
 表示a为数学期望,b为方差的高斯分布在c处的概率密度
表示a为数学期望,b为方差的高斯分布在c处的概率密度
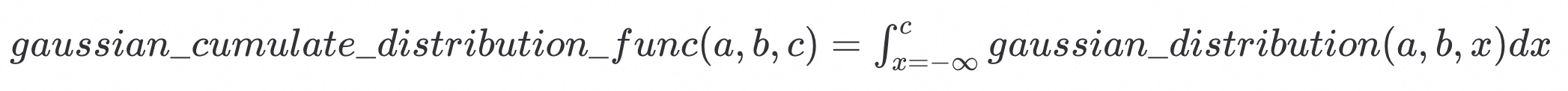
称为高斯累积分布函数
扫描行数(k)的求解方程为:

由于
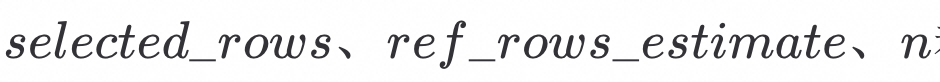 都是已知的,d_seq可用相关列的直方图简单推算
都是已知的,d_seq可用相关列的直方图简单推算
c可用correlation推算得到,因此可以求k的数值解,即为扫描行数
由correlation推算标准差
每个数据点的序偏离都满足高斯分布gaussian_distribution(0, c)
即,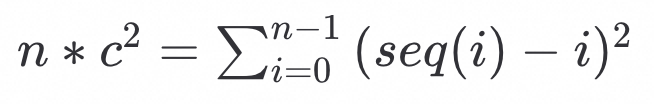
而correlation的计算公式(斯皮尔曼等级相关系数)为:
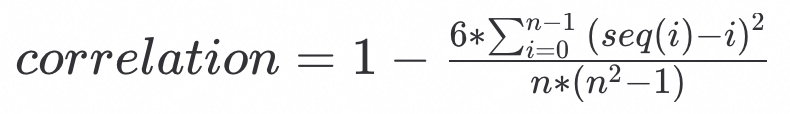
可以得到标准差c的近似求解公式:
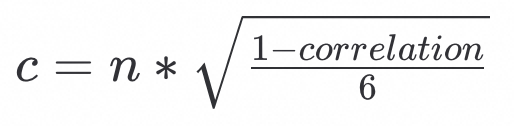
总结
求解公式为:
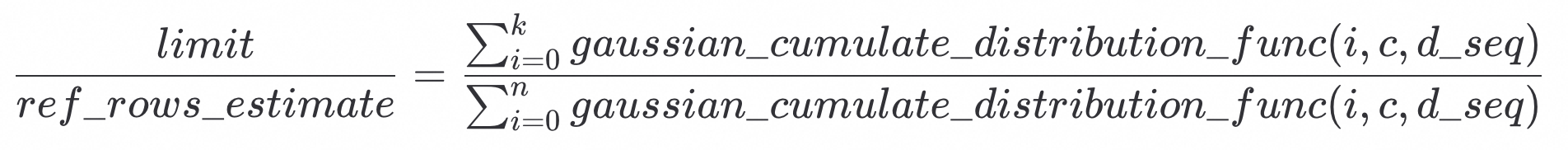
公式的左边是,limit所规定的选择率。
公式的右边是,顺序扫描ordering index,扫描到第k行的过程中符合相关条件(correlated_col_i < d)的数据,占全部符合相关条件的数据的比例。
这里只给出单相关条件的修正公式,如果多个列都存在相关性,情况将变得更加复杂。
效果
针对前文给出的两个case,这里给出新旧算法的估算结果,以及真实扫描行。
| case1 旧算法估算行数 | case1 新算法估算行数 | case1 真实扫描行数 | case2 旧算法估算行数 | case2 新算法估算行数 | case2 真实扫描行数 | |
|---|---|---|---|---|---|---|
| correlation = 0.999 | 107 | 9940 | 9892 | 107 | 2 | 2 |
| correlation = 0.95 | 38 | 7390 | 7637 | 38 | 5 | 2 |
| correlation = 0.84 | 22 | 4700 | 2936 | 22 | 5 | 3 |
| correlation = 0.71 | 15 | 2486 | 1873 | 15 | 5 | 2 |
数据构造逻辑: id列自增,time列在id列的基础上加高斯随机。