窗口函数Frame优化思想

背景

MySQL从8.0开始支持窗口函数（Window Functions），作用是计算一组聚合行的结果。其特点是可以同时具有分组和排序功能，且不改变原表行数，主要应用于数据分析场景。

本文将介绍下窗口函数Frame子句的优化思想，首先看下窗口函数示例:

SELECT SUM(c1) OVER (PARTITION BY c2 ORDER BY c3 ROWS BETWEEN x PRECEDING AND y FOLLOWING) FROM t;

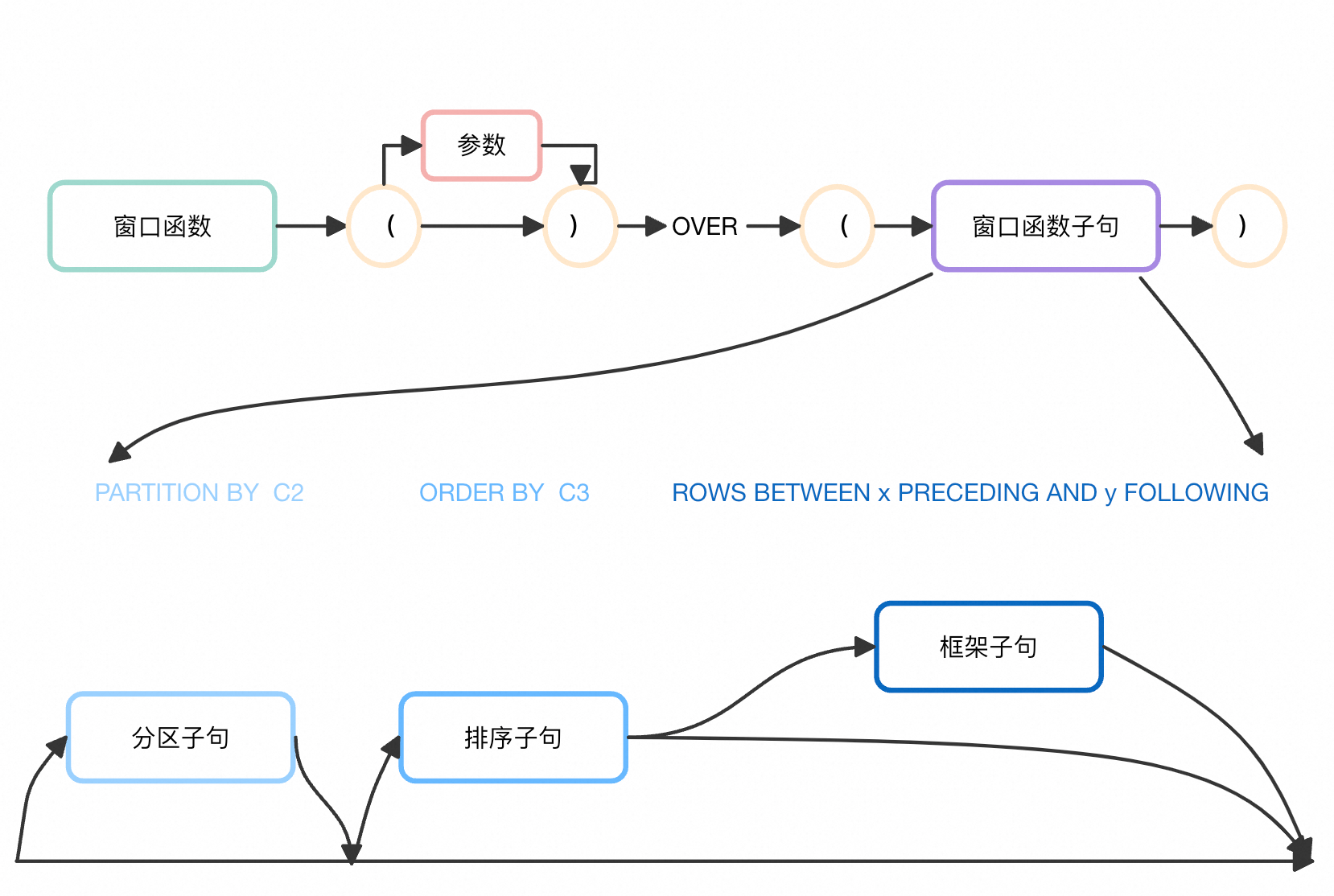
如图所示，图示为窗口函数的语法逻辑。其中窗口函数分为特有的窗口函数与聚合函数两类，窗口函数子句包含分区子句，排序子句和框架子句Frame。

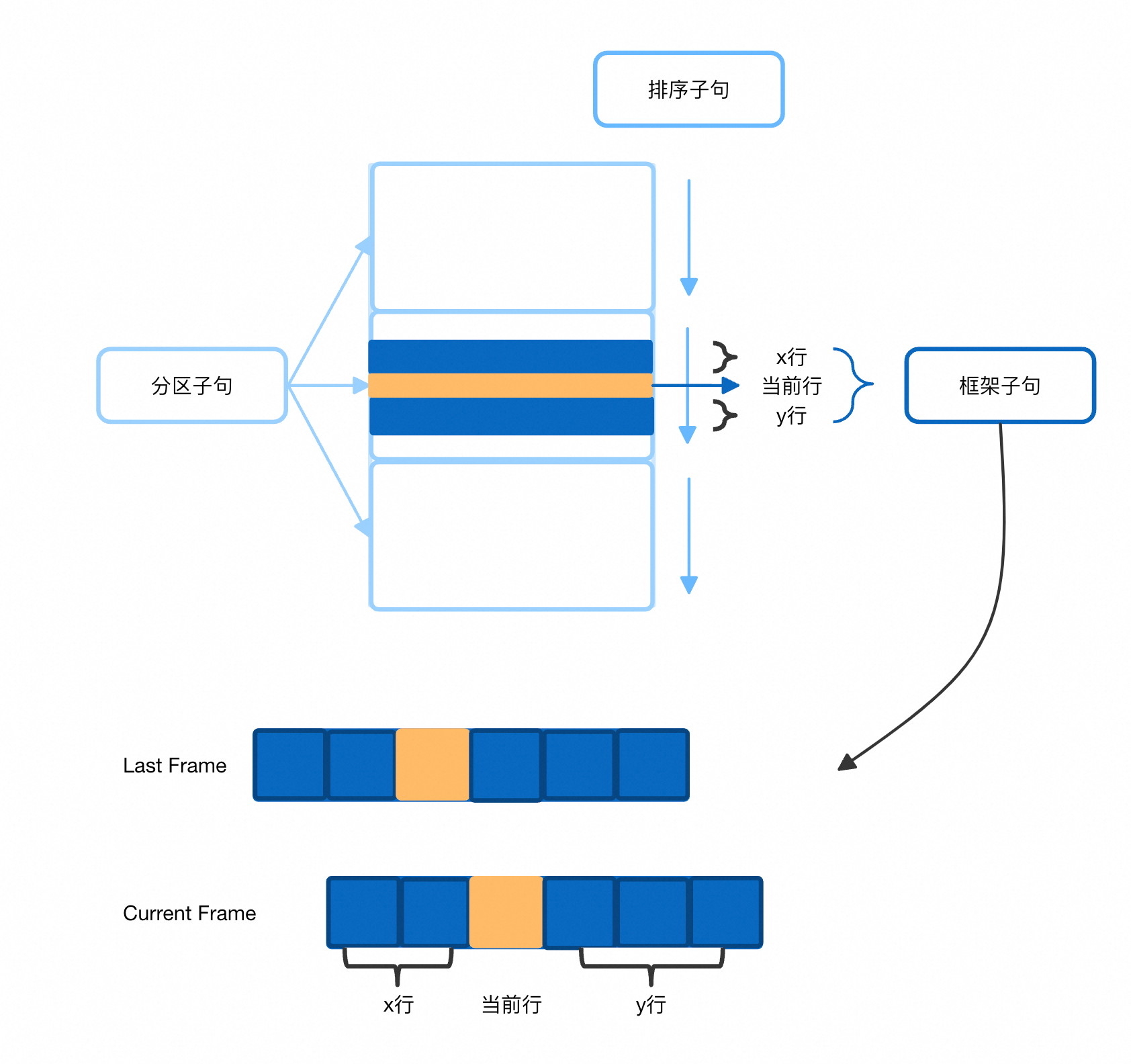
具体地，展开上述窗口函数子句，如上述case，我们首先基于c2 分区，c3 排序，每一个分区中，计算每一行时，会根据当前行构造frame区间，如当前case会从当前行向前数x行，向后数y行，最后计算x+y+1行的sum(c1)值。

默认场景下，每一行计算时，都需要先算出其Frame范围，并基于范围计算窗口函数值。一个分区遍历计算完，需要时间复杂度为O(N2). 考虑到当前行Frame与上一个的Frame关系，由此可以对Frame语句进行优化。

优化思想

由于窗口函数分为两类，其中一类为特有窗口函数，计算逻辑多与Frame无关，另一类为聚合函数，与Frame子句呈相关性，因此本文后续所述优化特指对聚合函数场景的Frame优化思想。

窗口函数Frame的计算主要分为默认的遍历计算，累加计算优化，可移除计算优化和线段树优化。其中本文将重点介绍前两种优化和简述线段树优化思想。

遍历计算：

默认的Frame计算方式，每一行Frame计算聚合函数值时，重新遍历当前Frame包含的窗口。

累加计算优化：

在Frame子句是ROWS BETWEEN UNBOUNDED PRECEDING AND CURRENT ROW时，我们可以复用Last Frame区间计算过的聚合值，如图所示：

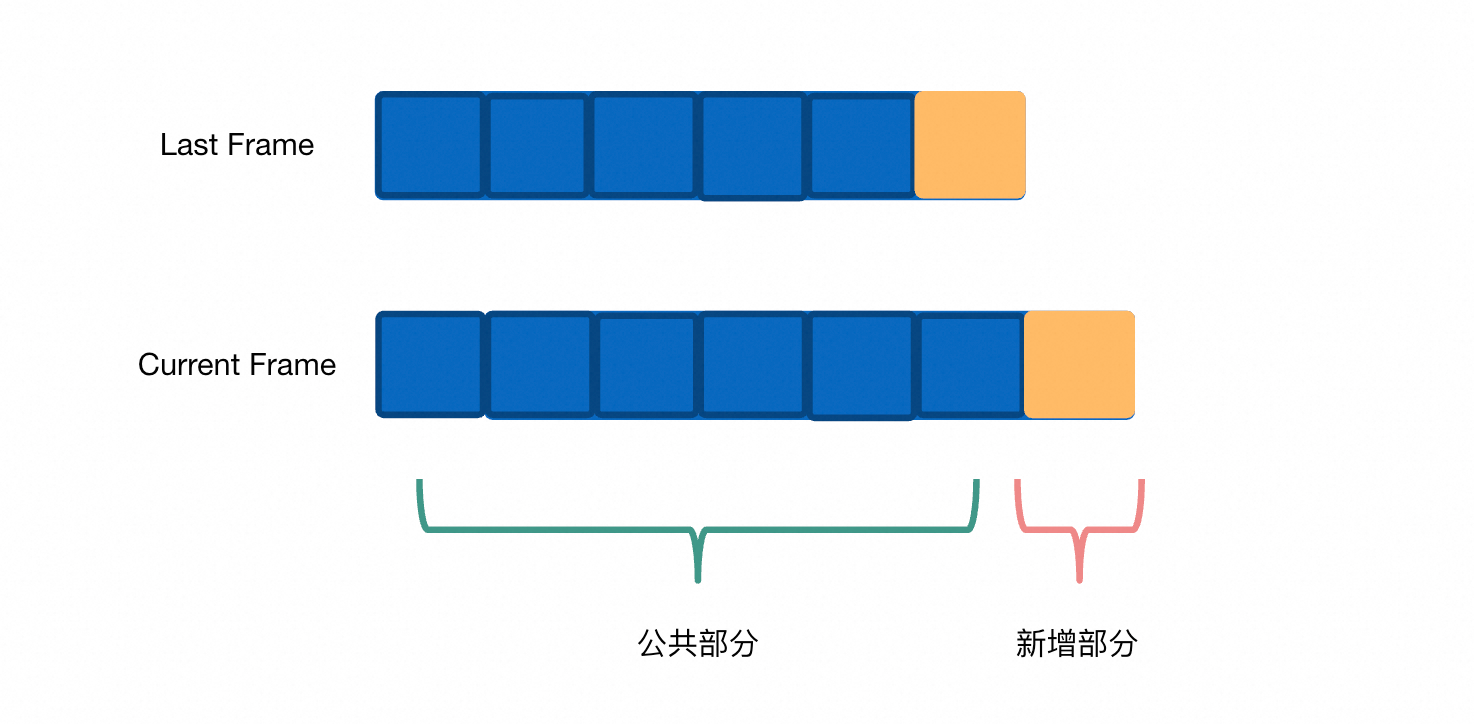
其中公共部分，Last Frame已经计算过聚合值，因此我们可以保留其聚合结果，在计算Current Frame时，我们只需要针对新增部分区间进行聚合结果计算即可，最终Current Frame的结果会由Last Frame结果 + 新增部分结果累加而得。

累加优化计算在此类特定场景下，可以服用Last Frame计算得到的聚合值，从而将时间复杂度从原先的O(N2)，优化为平均时间复杂度为O(N)，提升执行效率。

但是在Frame区间为滑动窗口场景时，无法使用此方法优化，只能回退为遍历计算。

可移除计算优化：

可移除计算优化思想，是为了解决累加计算无法应用的滑动窗口场景而提出。可移除优化思想根据聚合函数的不同细分为两类逻辑。其中一类为以Sum，Avg为代表的求和类聚合函数，另一类为以Max，Min为代表的极值类聚合函数。接下来分别介绍：

求和类聚合函数优化：

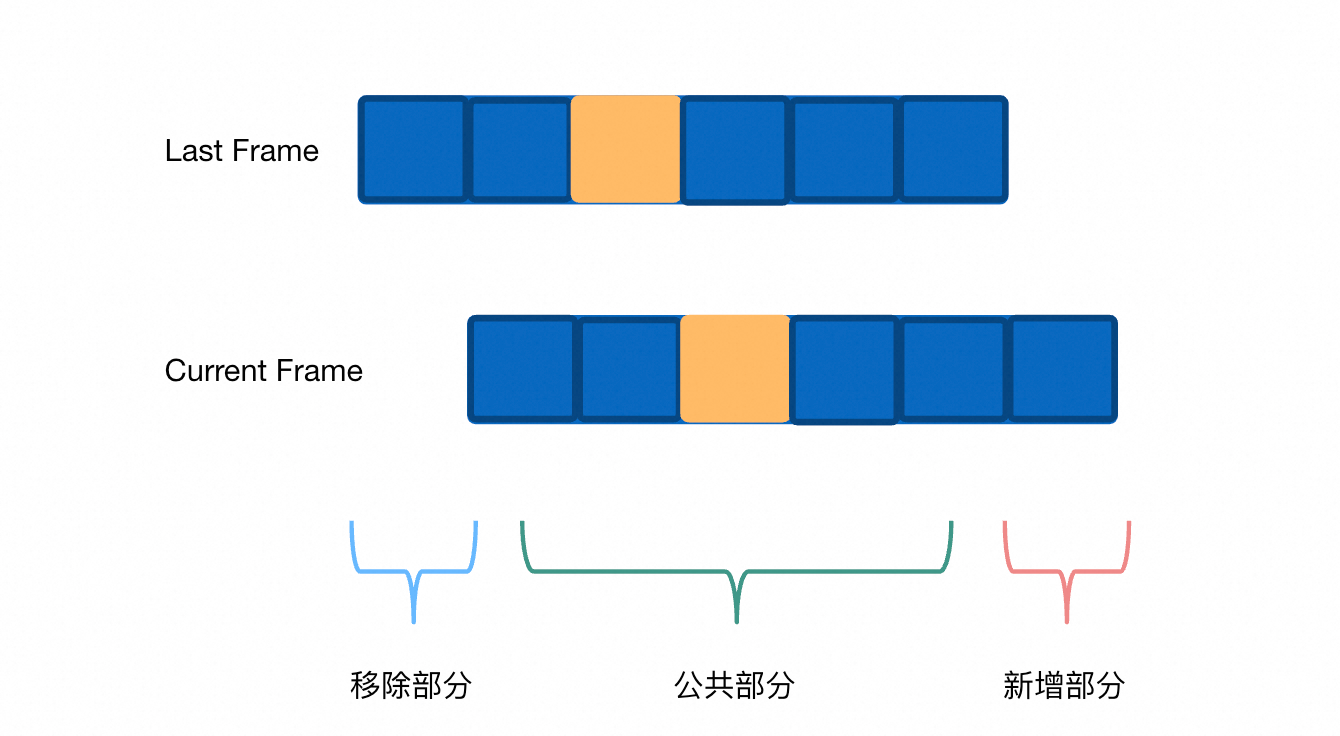
在Frame子句是ROWS BETWEEN 2 PRECEDING AND 3 FOLLOWING时，我们希望继续沿用累加计算的思想，如图所示：

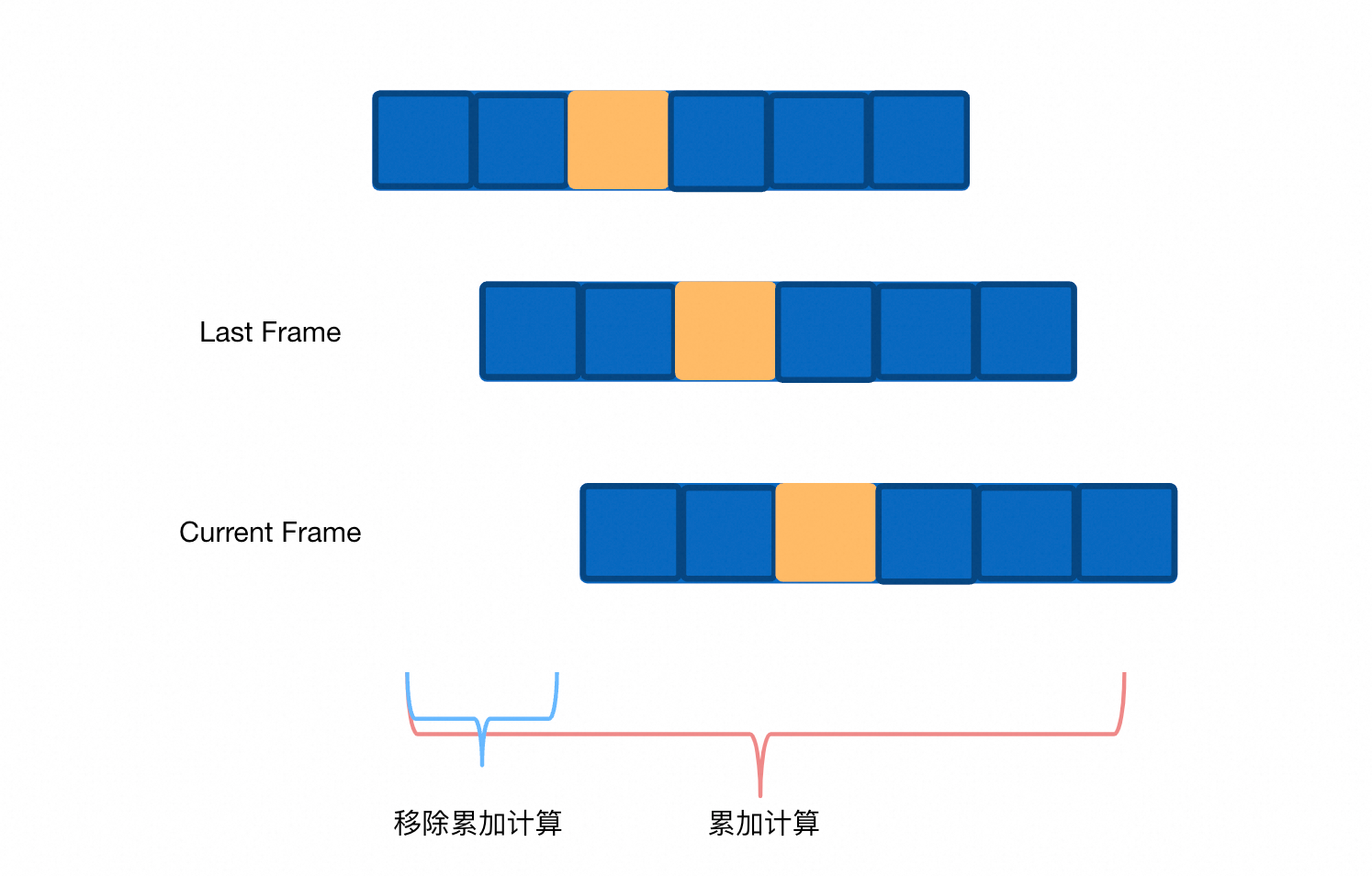
考虑到移除部分的求和类聚合函数也可以采用累加逻辑，因此我们采用两次累加计算结果取差值的方式，获取我们当前行的聚合结果值。

可移除优化复用了累加计算的思想，在Frame为滑动窗口下，平均时间复杂度优化至O(N)。当然上述思想仅限于求和类聚合函数的优化，因为极值类聚合函数场景，以Max函数为例，两次累加计算，只会记录Frame区间内的最大值，当滑动区间将最大值移除后，无法定位当前窗口的最大值。

极值类聚合函数优化：

在Frame子句是ROWS BETWEEN 2 PRECEDING AND 3 FOLLOWING时，我们设计新的优化思路，如图所示：

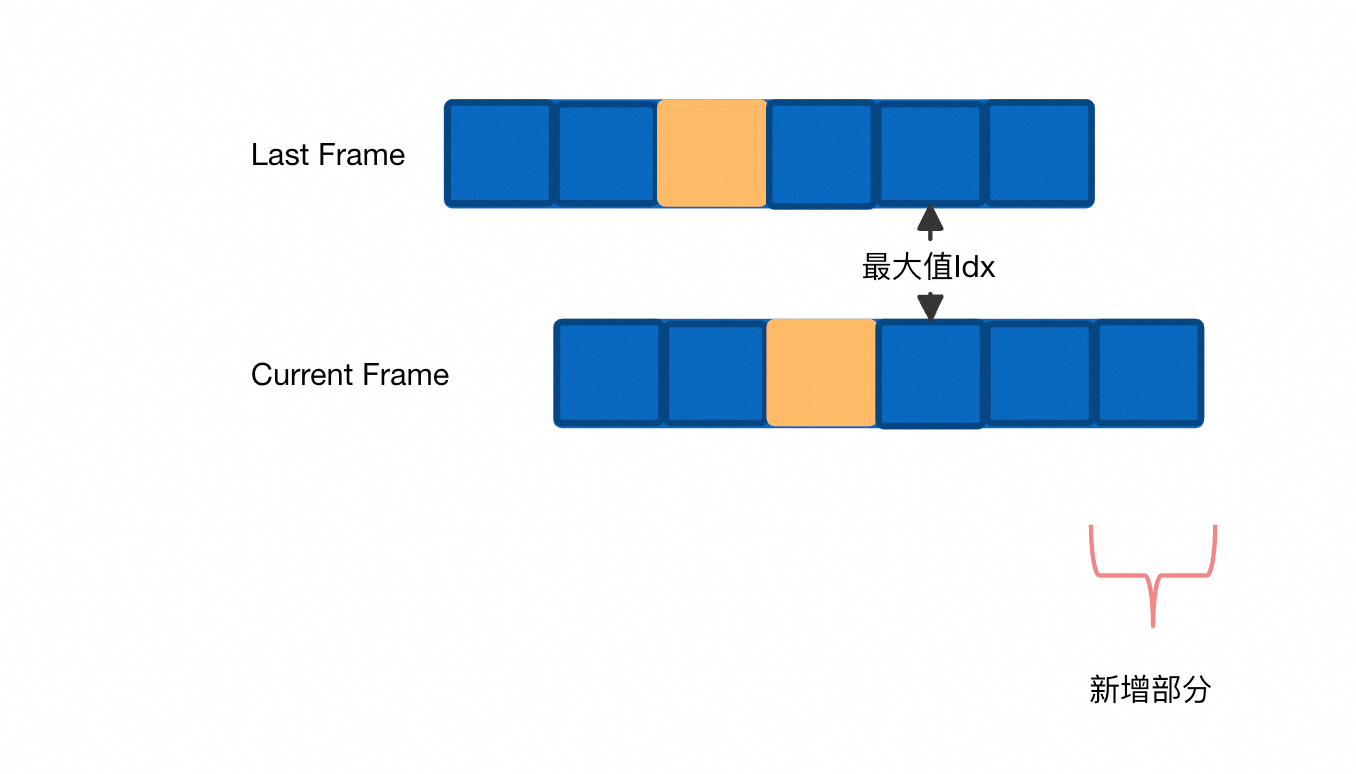
以Max函数为例，在计算最大值时，记录下最大值的Idx。此时分场景讨论，当最大值的Idx仍在Current Frame时，我们只需将最大值与新增部分比较，如果新增部分无更大的值，则Idx保持不变。如果新增部分存在更大的值，则更新最大值，并更新最大值的Idx。如果最大值的Idx不在Current Frame时，则需要重新遍历计算，更新最大值，并记录其Idx。

可移除优化这里考虑到真实数据场景最大值Idx，通常会存在于Frame区间范围，因此只需要将最大值与新增部分进行比较即可，平均时间复杂度优化为O(N)，极端场景下，会回退至O(N2)。

可移除优化思想可以满足MySQL的Frame优化场景，因为Frame子句中x和y参数只允许常量，不可以是变量场景。

线段树优化：

线段树优化更多地应用在Frame子句滑动窗口为变量滑动场景，由于Frame区间变动较大，累加计算和可移除计算优化通常会回退为遍历计算。

线段树优化的主要优化思想为针对每一个partition，首先构造线段树，预计算出整个partition的聚合值，当计算特定Frame时，从线段树中获取聚合函数值。时间复杂度会从O(N2)优化为O(NlogN)，是一种空间换时间的优化思想。具体优化思想可参考论文《Efficient Processing of Window Functions in Analytical SQL Queries》。

总结

本文主要介绍了窗口函数Frame的一些优化思想，其中累加计算与可移除计算优化，可以在不同的Frame场景，将时间复杂度从遍历计算的O(N2)，优化为平均时间复杂度O(N)。线段树优化在Frame子句为变量滑动窗口时，可以将时间复杂度从O(N2)，优化为时间复杂度O(NlogN)。

相关资料

《Efficient Processing of Window Functions in Analytical SQL Queries》。