MySQL · TokuDB · rbtree block allocator
Author: ruze
背景
Percona在今年8月引入了一个大patch “rb tree block allocation strategy”,使用变种的红黑树作为跟踪未使用block hole的数据结构。
Percona上对此介绍的连接(点击这里跳转到原文)
这个改进是基于percona内部性能测试和外部用户反馈,发现当TokuDB引擎在长时间写入压力比较大的场景下,随着时间增长写入性能会急剧下降;当采用small node size配置时(这是对高速存储设备场景下性能调优的建议),这个问题会更加严重。现象是:TPS降低,客户端的response time增加。
写入性能下降的主要原因是:原有的block allocator使用线性数组来记录已使用的blocks和最大未分配的block。每次分配的时候,顺序遍历已使用的blocks数组,按照strategy(first fit,best fit等四种strategy)找到一个未使用的block hole用来分配。当频繁写入,文件碎片比较多时,顺序遍历的代价就会非常大。
文件内部碎片化问题
为什么TokuDB索引文件碎片化比较严重? TokuDB缺省支持数据压缩,每个数据节点的partition分别压缩后顺序存储,导致数据节点的大小是变化的。其实在压缩之前,数据节点大小也不是一个固定值。中间节点除了包含pivot key,还包含msg buffer;空的中间节点可能就占几个字节,一个满的数据节点(既可以是中间节点也可以是叶子节点)可能占4M(缺省配置)。这跟传统使用btree(及其变种树)作为索引存储的数据库很不一样。数据节点大小是变化的,频繁创建/删除节点,会使得索引文件内部碎片化严重。另一方面,TokuDB的checkpoint机制也加剧了碎片化问题。
TokuDB的checkpoint过程对碎片化影响
TokuDB是sharp checkpoint,每次checkpoint(缺省是60秒执行一次)会把内存buffer pool中所有的脏页写到磁盘上。写采用非覆盖写,每次写到一个新的位置上。BTT(Block Translation Table)是一个数组,记录了blocknum到文件offset的映射。BTT的索引是blocknum,数组按照blocknum递增的顺序排列,每个数组元素记录了blocknum对应<offset,size>的二元组。
这里的blocknum是数据节点的逻辑页号,在数据节点的生命周期里始终不变,创建节点时生成,删除节点时被释放。 前面两节中谈到的block hole和block分配,其实分别是指索引文件中未使用的地址空间<offset,size>和分配索引文件中一段空闲的地址空间<offset,size>。
从磁盘读取节点时,需要查BTT确定blocknum在索引文件上的位置,然后seek到那个位置读数据;数据写回时,查找BTT找到满足节点大小的一个未使用的block hole,把节点数据写到那里。为了加速block hole的查找过程,TokuDB使用了线性数组_blocks_array来记录所有已经分配的blocks,数组按照offset递增顺序排列,每个数组元素仍然是<offset,size>的二元组。未使用的block hole是通过相邻的两个block之间的hole计算出来的: <b[n].offset + b[n].size, b[n+1].offset - (b[n].offset + b[n].size)>。
细心的朋友会发现,_blocks_array没有跟blocknum有关的信息,因为这个数组仅用于查找block hole。
这个patch改进的部分是把记录未分配block hole的数据结构,由原来的线性数组改造成红黑树,最差和平均的查找时间复杂度从o(n)变成o(logn)。
FT磁盘文件layout
Percona的文章里面谈到了FT文件layout,这里也简单介绍一下。其实这个patch,并没有修改BTT和 FT layout部分,数据文件与原来兼容。
TokuDB索引文件对应磁盘文件系统上一个独立的文件。 每个索引文件由3部分组成:header,BTT和blocks。Header 和 BTT都包含了多个版本。
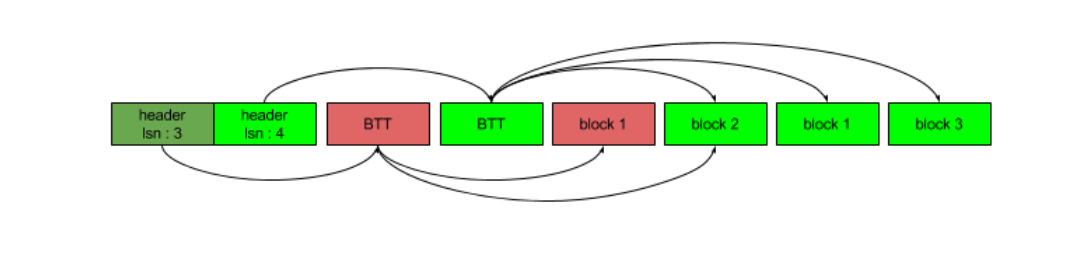
Header有2个版本:最近checkpoint的版本和更早checkpoint的版本。 BTT也有2个版本:最近checkpoint的版本和更早checkpoint的版本。
这2个版本的header位于索引文件固定位置上:offset 0和offset 4096。这两个header是以round robin的方式存储的,假若head 0是最近checkpoint的版本,head1就是更早checkpoint的版本;反之,head 0是更早checkpoint的版本,head1就是最近checkpoint的版本。
每个header里面保存着相应BTT的起始位置。如果想找到最近checkpoint的版本中blocknum 5在索引文件的位置,只要访问最近checkpoint的header找到对应BTT的起始位置,然后读取BTT找到blocknum 5对应的<offset,size>二元组,再seek到那个offset进行读取就可以了。
内存中FT的header也有2个版本:
- FT_CURRENT是当前的header
- FT_CHECKPOINT_INPROGRESS是checkpoint开始时刻FT_CURRENT的克隆
索引文件里面保存的2个header都是FT_CHECKPOINT_INPROGRESS,在checkpoint结束时被释放。
内存中的BTT有3个版本:
- TRANSLATION_CURRENT:当前的BTT
- TRANSLATION_INPROGRESS:checkpoint开始时刻TRANSLATION_CURRENT的克隆
- TRANSLATION_CHECKPOINTED:最近完成的checkpoint的BTT
Checkpoint结束时,释放TRANSLATION_CHECKPOINTED记录的映射关系,并把TRANSLATION_INPROGRESS拷贝给TRANSLATION_CHECKPOINTED。TRANSLATION_CHECKPOINTED记录了上一次完整checkpoint的数据,这些数据在新的checkpoint结束之前都是有效的,那些空间不允许被使用。
索引文件里面保存的2个BTT都是TRANSLATION_INPROGRESS,在checkpoint结束时被清空。
引入红黑树优化search time
Percona引入MHS (Max Hole Size)红黑树来解决这个问题。这是一个变种的红黑树,除了记录未使用的block hole,还存储了左右子树的max block size信息,在分配block hole的时候可以根据此信息进行减枝,避免不必要的子树遍历。
下面这个例子是percona给出的示例。
已分配blocks如下:

block holes如下:

红黑树如下:
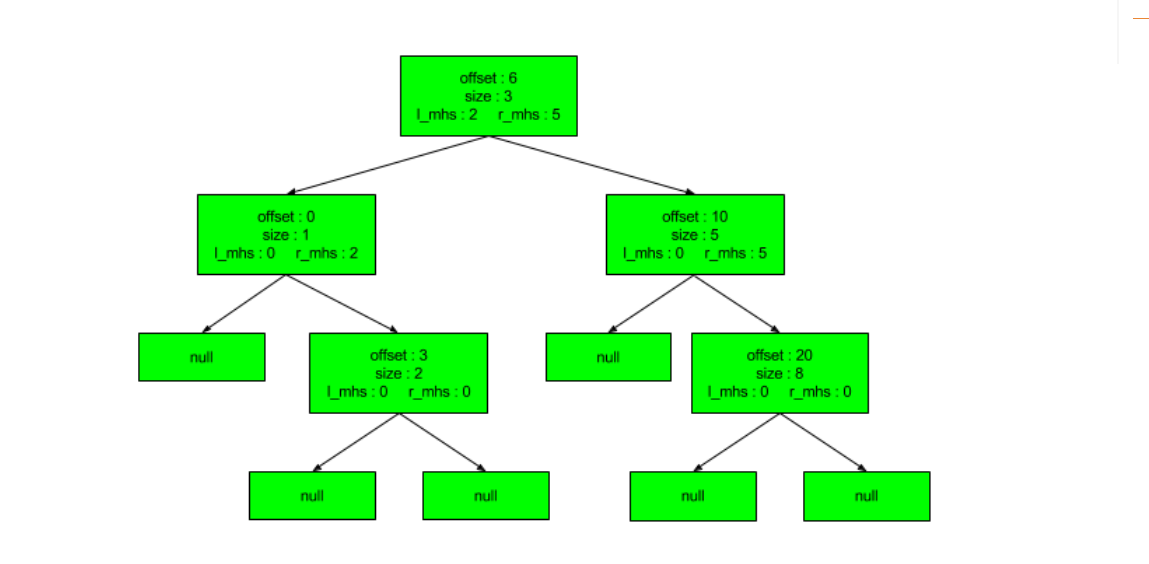
这个例子中,红黑树的数据节点存储的是已分配的block信息和左右子树的mhs信息。 但是,patch的代码实现的是:数据节点存储的是未使用的block信息和左右子树的mhs信息。 例子跟代码实现稍有差别,但是不影响示例的作用。
如果想分配4个字节的hole,只需要遍历root的右子树,不需要访问节点<0,1>和节点<3,2>,这极大的优化了block hole的搜索过程,从原来的o(n)变成o(logn),而且可以根据mhs信息进行适当减枝。
这个算法的缺点是:总是尝试从第一个满足条件的hole中分配,而不去看整个地址空间的使用情况。频繁small size分配会把地址空间的前部切分的非常细碎,小碎片情况可能会更加严重。
rbtree allocator实现
到这里,我们一起看一下rbtree allocator的实现。红黑树算法的部分比较复杂,也比较长,不打算在这里详细介绍了。如果有朋友感兴趣,我们可以另开一篇介绍。
从BTT的BlockPair数组构建rbtree
前面提到过这个patch没有修改BTT和FT layout,那么,自然可以用这个patch打开已有的FT索引文件。
当打开一个已有的FT索引文件时,首先去读FT header的信息。上一小结有提到过FT header有两个版本,TokuDB需要分别去读两个版本的header,看看是否都是有效的,哪个是更新的版本。
通过最新且有效的FT header,能够找到其对应的BTT的起始地址,读取每个blocknum到文件offset的映射信息生成BlockPair数组来构建allocator,这里是rbtree。
下面的函数就是通过BlockPair构建allocator的过程,首先是把BlockPair数组按照offset排序。之后,把排好序的BlockPair数组加到rbtree里面。
函数的第一个参数是reserve_at_beginning表示reserved的地址空间上限,通过allocator分配的block hole一定要大于reserve_at_beginning。所以,从reserve_at_beginning到排好序的BlockPair数组第一个元素之间也可能存在一个有效的hole,那也需要把它加到rbtree里面。
void BlockAllocator::CreateFromBlockPairs(uint64_t reserve_at_beginning,
uint64_t alignment,
struct BlockPair *translation_pairs,
uint64_t n_blocks) {
CreateInternal(reserve_at_beginning, alignment);
_n_blocks = n_blocks;
struct BlockPair *XMALLOC_N(n_blocks, pairs);
memcpy(pairs, translation_pairs, n_blocks * sizeof(struct BlockPair));
std::sort(pairs, pairs + n_blocks);
if (pairs[0]._offset > reserve_at_beginning) {
_tree->Insert(
{reserve_at_beginning, pairs[0]._offset - reserve_at_beginning});
}
for (uint64_t i = 0; i < _n_blocks; i++) {
// Allocator does not support size 0 blocks. See
// block_allocator_free_block.
invariant(pairs[i]._size > 0);
invariant(pairs[i]._offset >= _reserve_at_beginning);
invariant(pairs[i]._offset % _alignment == 0);
_n_bytes_in_use += pairs[i]._size;
MhsRbTree::OUUInt64 free_size(MAX_BYTE);
MhsRbTree::OUUInt64 free_offset(pairs[i]._offset + pairs[i]._size);
if (i < n_blocks - 1) {
MhsRbTree::OUUInt64 next_offset(pairs[i + 1]._offset);
invariant(next_offset >= free_offset);
free_size = next_offset - free_offset;
if (free_size == 0)
continue;
}
_tree->Insert({free_offset, free_size});
}
toku_free(pairs);
VALIDATE();
}
从rbtree分配block hole
从rbtree里面分配一个block hole,就是找到满足requested size的节点,从那里分配空间。之后,如果那个节点的size变成0,需要释放节点。其实这个过程就是从rbtree删除requested size大小的hole。
void BlockAllocator::AllocBlock(uint64_t size,
uint64_t *offset) {
// Allocator does not support size 0 blocks. See block_allocator_free_block.
invariant(size > 0);
_n_bytes_in_use += size;
*offset = _tree->Remove(size);
_n_blocks++;
VALIDATE();
}
Rbtree上删除size大小的hole是在函数Tree::Remove实现的。首先找到满足请求size的第一个hole,然后在hole上分配size,如果分配之后hole的size等于0,就要删除这个hole。
uint64_t Tree::Remove(size_t size) {
Node *node = SearchFirstFitBySize(size);
return Remove(_root, node, size);
}
如果root对应的hole不能满足请求size,并且左右子树mhs都比size小,表示root及其子树上都没有合适的空间,此时返回NULL表示在root上分配失败。
Node *Tree::SearchFirstFitBySize(uint64_t size) {
if (EffectiveSize(_root) < size && rbn_left_mhs(_root) < size &&
rbn_right_mhs(_root) < size) {
return nullptr;
} else {
return SearchFirstFitBySizeHelper(_root, size);
}
}
如果在root上有合适的空间分配,首先看一下root本身能否满足要求。
-
有种情况需要特殊处理,如果root本身可以满足分配,并且其左子树也可以满足分配。这种情况下优先在左子树上分配。
-
如果1失败,但是root本身能满足分配,此时在root上分配。
-
如果2失败,看看其左右子树是否满足分配;如果左右子树都能满足分配,优先在左子树上分配。
Node *Tree::SearchFirstFitBySizeHelper(Node *x, uint64_t size) {
if (EffectiveSize(x) >= size) {
// only possible to go left
if (rbn_left_mhs(x) >= size)
return SearchFirstFitBySizeHelper(x->_left, size);
else
return x;
}
if (rbn_left_mhs(x) >= size)
return SearchFirstFitBySizeHelper(x->_left, size);
if (rbn_right_mhs(x) >= size)
return SearchFirstFitBySizeHelper(x->_right, size);
// this is an invalid state
Dump();
ValidateBalance();
ValidateMhs();
invariant(0);
return NULL;
}
回到函数Tree::Remove,找到满足请求size的第一个节点后,需要从那个节点分配size大小的hole,也就是从那个节点删除size大小的空间。
从rbtree分配的block hole,是用来存放FT索引的数据节点的,为了支持direct I/O,分配的block hole的offset和size都必须是512的整数倍。
下面函数中,节点的n_offset,n_size表示的是rbtree节点的block hole的起始位置和大小,不一定是512对齐。answer_offset表示的才是512对齐的起始地址。
- 如果answer_offset不等于offset,分配之后一定有剩余,不需要删除节点,也不需要调整红黑树的形态。
分配之后: I. 可能只剩余<n_offset,answer_offset-n_offset>,相当于hole缩小; II. 可能剩余2个hole,512对齐前的一段<n_offset,answer_offset-n_offset>和分配size之后的一段<answer_offset+size, (n_offset + n_size)(answer_offset + size)>,相当于hole中间截断
在第二种情况,后面的hole是新产生的,需要加到红黑树里。
- 如果answer_offset等于offset,并且size等于n_size,分配之后需要把这个hole从红黑树里删除。
uint64_t Tree::Remove(Node *&root, Node *node, size_t size) {
OUUInt64 n_offset = rbn_offset(node);
OUUInt64 n_size = rbn_size(node);
OUUInt64 answer_offset(align(rbn_offset(node).ToInt(), _align));
invariant((answer_offset + size) <= (n_offset + n_size));
if (answer_offset == n_offset) {
rbn_offset(node) += size;
rbn_size(node) -= size;
RecalculateMhs(node);
if (rbn_size(node) == 0) {
RawRemove(root, node);
}
} else {
if (answer_offset + size == n_offset + n_size) {
rbn_size(node) -= size;
RecalculateMhs(node);
} else {
// well, cut in the middle...
rbn_size(node) = answer_offset - n_offset;
RecalculateMhs(node);
Insert(_root,
{(answer_offset + size),
(n_offset + n_size) - (answer_offset + size)});
}
}
return answer_offset.ToInt();
}
红黑树里,不会直接删除一个中间节点。 如果要删除的节点,左右子树都存在,需要找到它的直接后继,就是它的右子树上最左的节点。用那个节点代替它的位置,然后删除它。 如果它的左右子树只有一个是存在的,另一个为空,就用那个非空的子节点代替它。 删除过程会改变节点的位置,需要对受影响的节点重新计算mhs。 如果替代的节点是黑色的,需要调整树形态,满足每条路径上黑色节点的数目是相同的。
void Tree::RawRemove(Node *&root, Node *node) {
Node *child, *parent;
EColor color;
if ((node->_left != NULL) && (node->_right != NULL)) {
Node *replace = node;
replace = replace->_right;
while (replace->_left != NULL)
replace = replace->_left;
if (rbn_parent(node)) {
if (rbn_parent(node)->_left == node)
rbn_parent(node)->_left = replace;
else
rbn_parent(node)->_right = replace;
} else {
root = replace;
}
child = replace->_right;
parent = rbn_parent(replace);
color = rbn_color(replace);
if (parent == node) {
parent = replace;
} else {
if (child)
rbn_parent(child) = parent;
parent->_left = child;
rbn_left_mhs(parent) = rbn_right_mhs(replace);
RecalculateMhs(parent);
replace->_right = node->_right;
rbn_set_parent(node->_right, replace);
rbn_right_mhs(replace) = rbn_right_mhs(node);
}
replace->_parent = node->_parent;
replace->_color = node->_color;
replace->_left = node->_left;
rbn_left_mhs(replace) = rbn_left_mhs(node);
node->_left->_parent = replace;
RecalculateMhs(replace);
if (color == EColor::BLACK)
RawRemoveFixup(root, child, parent);
delete node;
return;
}
if (node->_left != NULL)
child = node->_left;
else
child = node->_right;
parent = node->_parent;
color = node->_color;
if (child)
child->_parent = parent;
if (parent) {
if (parent->_left == node) {
parent->_left = child;
rbn_left_mhs(parent) = child ? mhs_of_subtree(child) : 0;
} else {
parent->_right = child;
rbn_right_mhs(parent) = child ? mhs_of_subtree(child) : 0;
}
RecalculateMhs(parent);
} else
root = child;
if (color == EColor::BLACK)
RawRemoveFixup(root, child, parent);
delete node;
}
从rbtree释放block hole
当删除一个FT数据节点或者checkpoint结束时回收上次checkpoint占用的地址空间时,allocator需要记下这个block hole,把它加到红黑树里面。
void BlockAllocator::FreeBlock(uint64_t offset, uint64_t size) {
VALIDATE();
_n_bytes_in_use -= size;
_tree->Insert({offset, size});
_n_blocks--;
VALIDATE();
}
Rbtree insert的时候,跟binary tree一样,通过binary search找到合适的位置。找到以后,需要考虑是否能和相邻的hole合并。
新的hole可能只和它左边或者右边的hole合并;也可能同时跟左边和右边合并形成一个更大的hole。
这里,左边的hole就是它的直接前驱,右边的hole是它的直接后继。
如果可以合并,只需要修改已有rbtree节点的<offset,size>信息,不会引入新的节点。
如果不能合并,需要新加一个节点<offset,size>,然后加入到rbtree里。新加入的节点一定是红色的,由于引入新的红色节点,可能会导致连续的红色节点出现,需要调整红黑树的形态。
无论是合并了,还是引入新节点都需要对受影响节点重新计算mhs。
int Tree::Insert(Node *&root, Node::BlockPair pair) {
Node *x = _root;
Node *y = NULL;
bool left_merge = false;
bool right_merge = false;
Node *node = NULL;
while (x != NULL) {
y = x;
if (pair._offset < rbn_key(x))
x = x->_left;
else
x = x->_right;
}
// we found where to insert, lets find out the pred and succ for
// possible
// merges.
// node->parent = y;
Node *pred, *succ;
if (y != NULL) {
if (pair._offset < rbn_key(y)) {
// as the left child
pred = PredecessorHelper(y->_parent, y);
succ = y;
IsNewNodeMergable(pred, succ, pair, &left_merge, &right_merge);
if (left_merge || right_merge) {
AbsorbNewNode(
pred, succ, pair, left_merge, right_merge, false);
} else {
// construct the node
Node::Pair mhsp = {._left = 0, ._right = 0};
node =
new Node(EColor::BLACK, pair, mhsp, nullptr, nullptr, nullptr);
if (!node)
return -1;
y->_left = node;
node->_parent = y;
RecalculateMhs(node);
}
} else {
// as the right child
pred = y;
succ = SuccessorHelper(y->_parent, y);
IsNewNodeMergable(pred, succ, pair, &left_merge, &right_merge);
if (left_merge || right_merge) {
AbsorbNewNode(
pred, succ, pair, left_merge, right_merge, true);
} else {
// construct the node
Node::Pair mhsp = {._left = 0, ._right = 0};
node =
new Node(EColor::BLACK, pair, mhsp, nullptr, nullptr, nullptr);
if (!node)
return -1;
y->_right = node;
node->_parent = y;
RecalculateMhs(node);
}
}
} else {
Node::Pair mhsp = {._left = 0, ._right = 0};
node = new Node(EColor::BLACK, pair, mhsp, nullptr, nullptr, nullptr);
if (!node)
return -1;
root = node;
}
if (!left_merge && !right_merge) {
invariant_notnull(node);
node->_color = EColor::RED;
return InsertFixup(root, node);
}
return 0;
}