数据库内核月报

问题定义

Join graph

为了应用经典的图算法，我们需要通过join构建出一张图，该图的定义为

join语句中的每一个table都可以作为一个节点
join语句中的每一个predicate都可以作为一条边

Join tree

在经典的volcano模型中，每个query 会转成一颗树去执行，而join 部分也会转为其中的子树。不同的join tree对应不同的执行顺序，经典的join tree可以分为三类：left-deep、zig-zag 和 bushy

问题叙述

输入：一个join graph $G = (V, E)$

输出：一个join tree $T$，使得$C(T)$最小

\[T = Solve(G)\]

DP算法（bottom-up）

Join Ordering的动态规划算法可以避免无谓的计算，比如：

$C(R_1\Join R_2\Join R_3\Join R_4) > C(R_1\Join R_3\Join R_1\Join R_4) \\ if \space C(R_1\Join R_2\Join R_3) > C(R_1\Join R_3\Join R_2)$ 更形式化的描述是：

如果一个join tree T是最优的，那么T的每个子树也是最优的

根据上面的理论，我们可以确定DP算法的大致思路：

将大图划分为子图，首先求得子图的最优join tree
通过组合子图的join tree来进一步求得大图的join tree

比如一个join graph其可能有四个表${R_1, R_2, R_3, R_4}$，动态规划算法流程如下

我们先考虑集合大小为1的解
当求解集合大小为$k$ 的解时，我们会将其划分为一对子集来求解

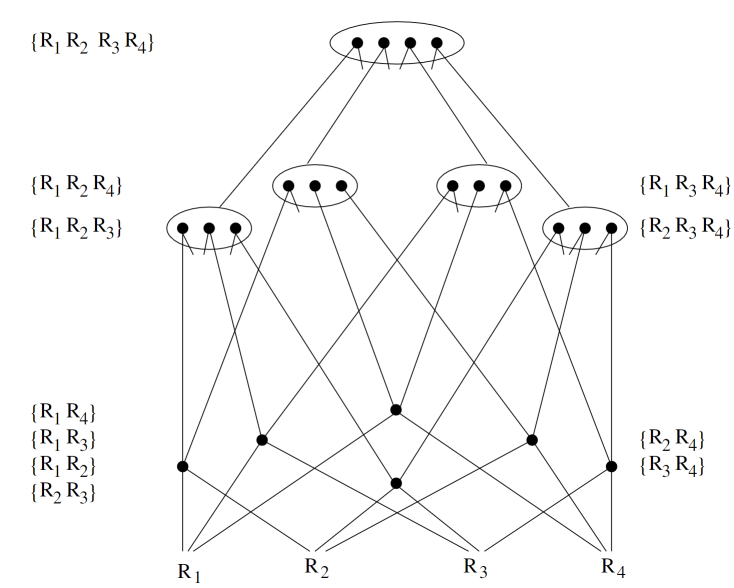
该算法需要注意

我们在将子集对的join tree合并成大的时，需要判断两个子集是否可以连接
不同的join tree对应不同的划分方式
1. 如果是left-deep tree，我们只需要结合大小为1和 大小为k-1的子树
2. 如果是bushy tree，如果需要考虑所有的组合情况

Dpccp：基于连通子图的枚举

上述算法考虑了所有可能的组合方案。然而，当join graph不是clique的时候，这些方案有很多不合法（两个子图不连通），为了避免这种不合法的方案，Dpccp被提出。 Dpccp的核心策略就是我们只会枚举一对连通的子图。更形式化的说法是

对于一个图$G=(V, E); V是点的集合，E是边的集合$，假设我们已经解出了一个子图$S_1$，我们需要枚举所有可能的子图$S_2$，$S_2$需要满足以下条件：

$S_1$和 $S_2$至少存在一条边相连：$\exist u \in S_1, \exist v \in S_2, (u, v) \in E$

$S_1$和$S_2$不相交

$S_1$和 $S_2$是连通图（连通图也就是其内部任意两个点都可以找到一条path连接）

而根据动态规划算法的要求，$S_2$还需要满足：

$S_2$存在一个最优解

在Dpccp里$S_1$被称之为csg（connect-subgraph），$S_2$被称之为cmp（complement），$(S_1, S_2)$也被称之为csg-cmp pair。由此我们可以得到基本的算法：

枚举补图

如果给定一个连通子图$S_1$，DPccp如何枚举它的子图？在算法中，我们是通过邻居节点来枚举补图的，步骤如下：

找到该csg的邻居节点：即该节点和$S_1$中的节点存在一条边相连
以邻居节点为起点，枚举出候选节点的所有的连通子图

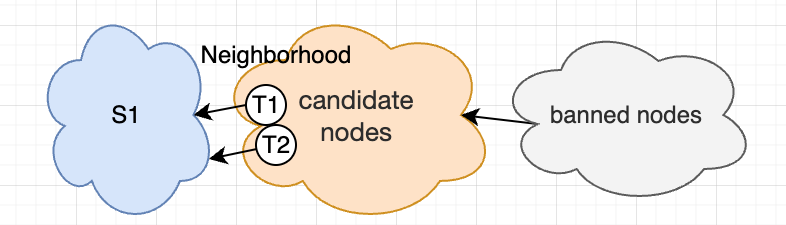
枚举顺序

在枚举csg-cmp-pair的时候，我们需要确定一个枚举顺序，使得

所有的子图和补图都枚举一遍
在枚举一个csg-cmp-pair $<S_1,S_2>$的时候，保证我们已经有$S_1, S_2$的最优解

为了满足上述要求Dpccp会给所有节点排序编号，即使得所有节点有全序关系。然后按照如下步骤枚举子图$S_1$：

按照从大到小的顺序确定一个初始节点$S ={u}$，其编号为$#u$
找到这个集合$S$的邻居集 $N$，将$N$的所有的子集加入$S$以扩张$S$
1. $N$中所有节点需要满足其编号 $\le #u$
递归的进行第二步

整体的算法步骤如下：

找到 csg
枚举csg的所有补图
用邻居扩张csg，然后对新的csg应用步骤2

问题

在join中，谓词可能会引用多个表：$T_1.x + T_2.y = T_3.x + T_4.y$（HyperGraph）

Dphyp: 基于hyper graph的枚举

为了解决谓词多多引用问题，Dphyp定义了HyperGraph。HyperGraph与上述Join Graph不同的是

在HyperGraph中，每个节点是表的集合，其可能包括一个或多个表，我们将其称之为hyper node

HyperGraph相比较普通的图而言，我们需要注意

在扩张子图的时候，每个hyper node要么全加入，要么不加入
Hyper node可能互相包含或者重叠

在Dpccp的时候，我们是通过找到Neighborhood节点，然后逐步加入Neighborhood节点来扩张子图的。所以我们的问题就是：

对于给定的子图 $S_1$，如何正确的计算它的相邻集合
给定相邻集合，我们如何得到合法的补图

编号

对于HyperGraph中的所有表（不是节点），我们同样将他们编号得到一个全序关系。对于每个hyper node，其编号为包含表的最小编号，记作：

相邻集合

首先我们给出对于子图$S$相邻集合的定义，其中$X$是排除掉的节点（比如编号小于起点的表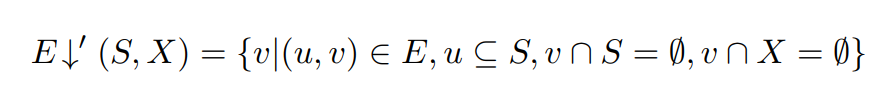）为了简化实现，我们可以只记录每个hyper node的编号，也就是

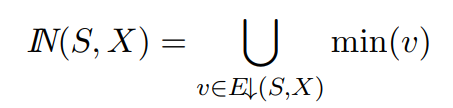
枚举补图

这样我们便可通过将这些编号作为起点来进一步的枚举出所有补图伪代码如下，该代码的功能是给定$S_1$，枚举其所有补图$S_2$。（其中$B_{min}(S_1) = {t | #t \geq min(S_1)}$）：

计算邻居节点
列举所有可以成为cmp的邻居节点
以邻居节点为初始集，扩张新的补图其中EnumerateCmpRec函数的功能是扩张补图$S_2$：
找到出事集的邻居节点集合
将集合加入$S_2$扩张 $S_2$
1. 列举出所有合法的$S_2$：
2. 进一步扩张$S_2$

去重

因为hyper node可能会存在包含或者重叠的关系，所以上述的枚举可能会做很多的冗余工作（比如对于$u_1 ={R_1, R_2, R_3}, u_2={R_2, R_3}$就会重复枚举${R_2, R_3}$）。

所以为了提高效率，我们需要尽量避免这种重复过程。已知在上述过程中，我们会让相邻表作为起点，然后逐步扩张它来生成子图。所以如果有多个hyper node重叠/包含，我们只需要保存一个表即可。

代码实现

数据结构

在Hyper graph中，没个表用其编号（实际就是索引）表示

每个边包含其链接的hyper node，每个hyper node使用位图表示（如果这条边的节点只包含一个表，被称为simple edge）

struct Hyperedge {
    // The endpoints (hypernodes) of this hyperedge. See the comment about
    // duplicated edges in Node.
    //
    // left and right may not overlap, and both must have at least one bit set.
    NodeMap left;
    NodeMap right;
};

每个节点Node包含所有引用自己的边：

struct Node {
  std::vector<unsigned> complex_edges, simple_edges;
  NodeMap simple_neighborhood = 0;
};

HyperGraph就是持有所有边和节点的结构体：

struct Hypergraph {
  std::vector<Node> nodes;  // Maximum 8*sizeof(NodeMap) elements.
  std::vector<Hyperedge> edges;
};

流程入口

入口代码：

AccessPath *FindBestQueryPlan(THD *thd, Query_block *query_block, string *trace) {
    MakeJoinHypergraph();
    if (EnumerateAllConnectedPartitions()) {
        SimplifyQueryGraph();
        EnumerateAllConnectedPartitions());
    }
    .....construct access path
}

构建HyperGraph

自底向上的构建节点和边

bool MakeJoinHypergraph(THD *thd, string *trace, JoinHypergraph *graph) {
    // 1. 构建expression tree
    RelationalExpression *root =
      MakeRelationalExpressionFromJoinList(thd, query_block->top_join_list);
    // 2. 谓词下推:对于无法推到 join/table 中到where 条件，会构建出inner join
    PushDownJoinConditions(thd, root, table_num_to_companion_set, &table_filters,
                         &cycle_inducing_edges, trace);
    // 3. 构建HyperGraph
    MakeJoinGraphFromRelationalExpression(thd, root, trace, graph);
}

void MakeJoinGraphFromRelationalExpression(THD *thd, RelationalExpression *expr,
                                           string *trace,
                                           JoinHypergraph *graph) {
  if (expr->type == RelationalExpression::TABLE) {
    graph->nodes.push_back(JoinHypergraph::Node{expr});
    return;
  }

  MakeJoinGraphFromRelationalExpression(thd, expr->left, trace, graph);
  MakeJoinGraphFromRelationalExpression(thd, expr->right, trace, graph);
  const Hyperedge edge = FindHyperedgeAndJoinConflicts(thd, used_nodes, expr);
  graph->graph.AddEdge(edge.left, edge.right);
}

构建边（基于CD-C冲突检测算法）

Hyperedge FindHyperedgeAndJoinConflicts(THD *thd, NodeMap used_nodes,
  Mem_root_array<ConflictRule> conflict_rules(thd->mem_root);
  ForEachJoinOperator(
      expr->left, [expr, &conflict_rules](RelationalExpression *child) {
        if (!OperatorsAreAssociative(*child, *expr)) {
          const NodeMap left = IntersectIfNotDegenerate(
              child->conditions_used_tables, child->left->nodes_in_subtree);
          conflict_rules.push_back(
              ConflictRule{child->right->nodes_in_subtree, left});
        }
        if (!OperatorsAreLeftAsscom(*child, *expr)) {
          const NodeMap right = IntersectIfNotDegenerate(
              child->conditions_used_tables, child->right->nodes_in_subtree);
          conflict_rules.push_back(
              ConflictRule{child->left->nodes_in_subtree, right});
        }
      });

  ForEachJoinOperator(
      expr->right, [expr, &conflict_rules](RelationalExpression *child) {
        if (!OperatorsAreAssociative(*expr, *child)) {
          const NodeMap right = IntersectIfNotDegenerate(
              child->conditions_used_tables, child->right->nodes_in_subtree);
          conflict_rules.push_back(
              ConflictRule{child->left->nodes_in_subtree, right});
        }
        if (!OperatorsAreRightAsscom(*expr, *child)) {
          const NodeMap left = IntersectIfNotDegenerate(
              child->conditions_used_tables, child->left->nodes_in_subtree);
          conflict_rules.push_back(
              ConflictRule{child->right->nodes_in_subtree, left});
        }
      });

  NodeMap total_eligibility_set =
      AbsorbConflictRulesIntoTES(used_nodes, &conflict_rules);

  if (!Overlaps(total_eligibility_set, expr->left->nodes_in_subtree)) {
    total_eligibility_set |= expr->left->nodes_in_subtree;
    total_eligibility_set =
        AbsorbConflictRulesIntoTES(total_eligibility_set, &conflict_rules);
  }
  if (!Overlaps(total_eligibility_set, expr->right->nodes_in_subtree)) {
    total_eligibility_set |= expr->right->nodes_in_subtree;
    total_eligibility_set =
        AbsorbConflictRulesIntoTES(total_eligibility_set, &conflict_rules);
  }
  expr->conflict_rules = std::move(conflict_rules);

  const NodeMap left = total_eligibility_set & expr->left->nodes_in_subtree;
  const NodeMap right = total_eligibility_set & expr->right->nodes_in_subtree;
  return {left, right};
}

DPhyp 算法

入口函数：

bool EnumerateAllConnectedPartitions(const Hypergraph &g, Receiver *receiver) {
  for (int seed_idx = g.nodes.size() - 1; seed_idx >= 0; --seed_idx) {
    NodeMap seed = TableBitmap(seed_idx);
    NodeMap forbidden = TablesBetween(0, seed_idx);
    NodeMap full_neighborhood = 0;
    NeighborhoodCache cache(0);
    // 1. 找到邻居节点
    NodeMap neighborhood =
        FindNeighborhood(g, seed, forbidden, seed, &cache, &full_neighborhood);
    // 2.枚举所有到补图
    EnumerateComplementsTo(g, seed_idx, seed, full_neighborhood,
                               neighborhood, receiver));
    // 3. 扩张子图，然后再继续枚举补图
    ExpandSubgraph(g, seed_idx, seed, full_neighborhood, neighborhood,
                       forbidden | seed, receiver));
  }
  return false;
}

计算邻居节点

和上述伪代码完全一致，不过这里引入了一个新的数据结构full_neighborhood，该数据结构用于来判定后面的补图和子图是否连通。

inline NodeMap FindNeighborhood(const Hypergraph &g, NodeMap subgraph,
                                NodeMap forbidden, NodeMap just_grown_by,
                                NeighborhoodCache *cache,
                                NodeMap *full_neighborhood_arg) {
  NodeMap full_neighborhood =
      *full_neighborhood_arg;  // Keep us out of aliasing trouble.
  NodeMap neighborhood = 0;

  NodeMap to_search =
      cache->InitSearch(just_grown_by, &neighborhood, &full_neighborhood);
  
  for (size_t node_idx : BitsSetIn(to_search)) {
    // Simple edges.
    // NOTE: This node's simple neighborhood will be added lazily to
    // full_neighborhood below. Forbidden nodes will also be removed below.
    neighborhood |= g.nodes[node_idx].simple_neighborhood;

    // Now go through the complex edges and see which ones point out of the
    // subgraph.
    for (size_t edge_idx : g.nodes[node_idx].complex_edges) {
      const Hyperedge e = g.edges[edge_idx];

      if (IsSubset(e.left, subgraph) &&
          !Overlaps(e.right, subgraph | forbidden)) {
        // e.right is an interesting hypernode (part of E↓'(S,X)).
        full_neighborhood |= e.right;
        if (!Overlaps(e.right, neighborhood)) {
          neighborhood |= IsolateLowestBit(e.right);
        }
      }
    }
  }

  neighborhood &= ~(subgraph | forbidden);
  full_neighborhood |= neighborhood;
  full_neighborhood_arg = full_neighborhood;
  return neighborhood;
}

枚举补图

template <class Receiver>
[[nodiscard]] bool EnumerateComplementsTo(
    const Hypergraph &g, size_t lowest_node_idx, NodeMap subgraph,
    NodeMap full_neighborhood, NodeMap neighborhood, Receiver *receiver) {
  
  NodeMap forbidden = TablesBetween(0, lowest_node_idx);
  for (size_t seed_idx : BitsSetInDescending(neighborhood)) {
    // 1. 首先考虑simple node（也就是指包括一个表的hyper node）
    // 1.1. simple node <-> simple node
    NodeMap seed = TableBitmap(seed_idx);
    if (Overlaps(g.nodes[seed_idx].simple_neighborhood, subgraph)) {
      // 1.1.1 找到对应的那条边
      for (size_t edge_idx : g.nodes[seed_idx].simple_edges) {
        const Hyperedge e = g.edges[edge_idx];
        if (Overlaps(e.right, subgraph)) {
          // 1.1.2 将csg（subgraph）-cmp（seed）-pair加入dpTable中
          receiver->FoundSubgraphPair(subgraph, seed, edge_idx / 2));
        }
      }
    }
    // 1.2 simple node <-> complex node
    for (size_t edge_idx : g.nodes[seed_idx].complex_edges) {
      const Hyperedge e = g.edges[edge_idx];
      if (e.left == seed && IsSubset(e.right, subgraph)) {
        receiver->FoundSubgraphPair(subgraph, seed, edge_idx / 2));
      }
    }
    
    // 2. 继续扩张补图来进一步完成枚举（感觉这里不应该将TablesBetween(0, seed_idx)加入forbidden）
    NodeMap new_forbidden =
        forbidden | subgraph | (neighborhood & TablesBetween(0, seed_idx));
    NodeMap new_full_neighborhood = 0;  // Unused; see comment on TryConnecting.
    NodeMap new_neighborhood = FindNeighborhood(g, seed, new_forbidden, seed,
                                                &cache, &new_full_neighborhood);
    ExpandComplement(g, lowest_node_idx, subgraph, full_neighborhood, seed,
                         new_neighborhood, new_forbidden, receiver));
  }
  return false;
}

如果判断子图和补图链接

template <class Receiver>
[[nodiscard]] bool TryConnecting(const Hypergraph &g, NodeMap subgraph,
                                 NodeMap subgraph_full_neighborhood,
                                 NodeMap complement, Receiver *receiver) {
  for (size_t node_idx : BitsSetIn(complement & subgraph_full_neighborhood)) {
    // 1. 遍历所有既在补图又在full neighborhod中的节点
    // 2. 查看它们是否存在一条边，使得这条边的一个节点完整的包含在子图内
    // Simple edges.
    if (Overlaps(g.nodes[node_idx].simple_neighborhood, subgraph)) {
      for (size_t edge_idx : g.nodes[node_idx].simple_edges) {
        const Hyperedge e = g.edges[edge_idx];
        if (Overlaps(e.right, subgraph) && Overlaps(e.left, complement)) {
          receiver->FoundSubgraphPair(subgraph, complement, edge_idx / 2));
        }
      }
    }

    // Complex edges.
    NodeMap node = TableBitmap(node_idx);
    for (size_t edge_idx : g.nodes[node_idx].complex_edges) {
      const Hyperedge e = g.edges[edge_idx];

      // NOTE: We call IsolateLowestBit() so that we only see the edge once.
      if (IsolateLowestBit(e.left) == node && IsSubset(e.left, complement) &&
          IsSubset(e.right, subgraph)) {
        receiver->FoundSubgraphPair(subgraph, complement, edge_idx / 2)
      }
    }
  }
  return false;
}

扩张子图

template <class Receiver>
[[nodiscard]] bool ExpandSubgraph(const Hypergraph &g, size_t lowest_node_idx,
                                  NodeMap subgraph, NodeMap full_neighborhood,
                                  NodeMap neighborhood, NodeMap forbidden,
                                  Receiver *receiver) {
 // 1. 针对那些已经求得最优解的子图，我们可以去枚举它们的补图 
 for (NodeMap grow_by : NonzeroSubsetsOf(neighborhood)) {
    NodeMap grown_subgraph = subgraph | grow_by;
    if (receiver->HasSeen(grown_subgraph)) {
      NodeMap new_full_neighborhood = full_neighborhood;
      NodeMap new_neighborhood =
          FindNeighborhood(g, subgraph | grow_by, forbidden, grow_by, &cache,
                           &new_full_neighborhood);
      new_neighborhood |= forbidden & ~TablesBetween(0, lowest_node_idx);
      new_neighborhood |= neighborhood;
      EnumerateComplementsTo(g, lowest_node_idx, grown_subgraph,
                                 new_full_neighborhood, new_neighborhood,
                                 receiver))
      }
    }
  }
  // 2. 进一步去扩张csg
  for (NodeMap grow_by : NonzeroSubsetsOf(neighborhood)) {
    NodeMap grown_subgraph = subgraph | grow_by;

    NodeMap new_forbidden = (forbidden | neighborhood) & ~grown_subgraph;
    
    NodeMap new_full_neighborhood = full_neighborhood;
    NodeMap new_neighborhood =
        FindNeighborhood(g, subgraph | grow_by, new_forbidden, grow_by, &cache,
                         &new_full_neighborhood);

    ExpandSubgraph(g, lowest_node_idx, grown_subgraph,
                       new_full_neighborhood, new_neighborhood, new_forbidden,
                       receiver));
    }
  }
  return false;
}

数据库内核月报－ 2022 / 06

MySQL中的HyperGraph优化器

问题定义

Join graph

Join tree

问题叙述

DP算法（bottom-up）

Dpccp：基于连通子图的枚举

枚举补图

枚举顺序

问题

Dphyp: 基于hyper graph的枚举

编号

相邻集合

枚举补图

去重

代码实现

数据结构

流程入口

构建HyperGraph

DPhyp 算法

计算邻居节点

枚举补图

扩张子图