PolarDB-PG 实时物化视图如何支持 outer join
Author: 林烁
写在前面:
本文将介绍 PolarDB PG 如何在现有的实时物化视图框架中支持 outer join 算子。
内容主要聚焦于原理部分,背景和具体实现细节将不再展开。
基本原理参考如下论文和技术报告:
-
论文:https://www.cs.columbia.edu/~jrzhou/pub/OJViewMaintenance.pdf
-
技术报告:https://www.microsoft.com/en-us/research/wp-content/uploads/2005/06/tr-2005-78.pdf
欢迎随时交流讨论,文档中任何有误之处欢迎指正🫡
背景
本节介绍物化视图支持 outer join 等算子的背景。
基本概念
物化视图的概念
如何理解物化视图?(Materialized View,MV)
视图是一种虚拟表,而物化视图本质是一种包含SQL查询结果的物理表,通过以存代算的方式实现查询加速。
物化视图的维护更新
我们知道物化视图带来了查询性能的提升,但也引入了维护的开销。
当物化视图的数据对应的表或分区产生插入、覆写、更新、删除等操作时,物化视图会自动失效,因此需要进行更新。
- 按照更新范围分类
-
全量更新
- 相当于重新执行一遍查询得到结果
-
增量更新(Incremental View Maintenance, IVM)对应插件 polar_ivm
-
利用基表变更产生的增量,计算出物化视图的增量
-
保持实时物化视图与基表的数据一致性
-
- 按照更新时机分类
-
实时更新(同步)
-
延迟更新(异步)
当前我们关注的是 实时 + 增量 更新机制。
场景介绍
背景可以概括为两个关键词:实时 + 分析
-
实时:越来越多的业务从传统的离线批处理转向在线流式更新,这些业务对时效性的要求很高。
-
分析:在实时更新的基础上,客户会有很多具体的分析需求。
功能上,PG 此前已经支持了 inner join、常见的聚合函数(min/max/avg/sum/count)、distinct 算子。
但是实时物化视图的使用仍有很多使用限制,例如不支持以 left join 为代表的 outer join,这一点极大的限制了实时物化视图的客户使用,多次有客户反馈希望支持这个功能。
增量更新基本原理
本节介绍增量更新的必要性以及当前 PG 框架的基本流程。
增量更新的必要性
物化视图本质上是一张包含SQL查询结果的物理表。因此当基表发生变更时,我们需要对物化视图进行更新。
具体更新维护有两种方式:
-
全量更新
-
增量更新
为了满足实时性需求,我们选择计算量更小的增量更新方式。
问题描述
物化视图的增量更新,实际上可以抽象为:已知基表变更、物化视图定义(相当于一条query),求解物化视图增量的数学问题。
不同类型的算子,其增量的计算方式也各不相同。
整体流程
三阶段流程
当前 PG 的增量更新整体框架如下:
当某个基表发生变更时,更新框架可以被简单地概括为三个阶段:
-
获取基表增量
-
计算物化视图增量(核心)
-
应用物化视图增量
多表计算规则
如果用户在同一个事务或单条 SQL 中修改了多个基表,则需要按照特定规则依次更新物化视图。
假设现在 A B C 三张基表都发生修改,对应的增量记为$\Delta A, \Delta B, \Delta C$,那么物化视图的增量为:
这里的$A$表示更新前的状态(preupdate state),而$A + \Delta A$表示更新后的状态(postupdate state)。
如何证明?
我们可以把这三项加起来,化简得到最终的增量:
$\Delta_{mv} = \Delta{mv_A} + \Delta{mv_B} +\Delta{mv_C} = (A + \Delta A) {\Join} (B + \Delta B) {\Join} (C + \Delta C) - A{\Join} B {\Join} C$
增量更新支持 outer join 原理
概述
难点分析
和原有支持 inner join 的方案对比,支持 outer join 的处理框架和原有框架基本一致,区别和难点在于:引入空值填充的语义后,空值 null 如何处理?
下面这个例子中,可以观察到:
-
基表中删除一行,物化视图中除了删除对应的行,还可能要插入一些因不匹配产生的空值填充行。
-
同理,基表中插入一行后,物化视图中除了插入匹配成功的行,还可能要删除一些原来不匹配的空值填充行。
inner join 只处理完全匹配的情况,因此会忽略所有空值填充行。
因此,到了 outer join,我们需要一套专门的算法,额外的引入一些辅助数据结构,帮我们找到空值行有哪些。
框架扩展
引入 outer join 后,在当前框架整体流程中,步骤 3(增量计算阶段)发生了扩展(如下图):
具体步骤我们后面讲完原理再回头探究。
引例
先看一个具体的例子。
假设用于定义物化视图的query是三表连接关系:
$query = R \overset{\text{left}}{\underset{R.A = T.A}{\Join}} T \overset{\text{full}}{\underset{T.B = S.B}{\Join}} S$
-
先解释下符号含义:
-
R, T, S代表三张表
-
A, B代表属性列
-
left:左外连接
-
full:全外连接
-
- 假设初始时各个表有数据:
$R(A) = {a1, a2} \ T(A, B) = {(a1, b1)} \ S(B) = {b1, b3}$
-
那么根据 query 定义,(口算)得到的查询结果,也就是物化视图的初始状态为:

-
假设在表T上发生了一次删除操作,删除一条 tuple:$\Delta T = {(a1, b1)}$
我们来看mv应该如何更新:
-
step1:首先,$\varDelta T = {(a1, b1)}$对应的行$(a1, (a1, b1), b1)$应该被删除
-
step2:其次,补充两条填充 null 值的行$(a1, (null, null), null), (null, (null, null), b1)$

- 假设在表T上发生了一次插入操作,插入一条新tuple:$\varDelta T = {(a2, b2)}$
我们来看mv应该如何更新:
-
step1:首先,需要插入新的一行$(a2, (a2, b2), b2)$
-
step2:其次,原有的冗余行会被覆盖$(a2, (null, null), null)$

至此,这个例子的增量物化视图的更新已经完成👋
规律总结
观察例子,我们可以发现两个重要的规律:
❶ 规律一:
每次对物化视图的更新,都可以分为两阶段:
-
先根据视图定义中表之间的连接关系,插入/删除匹配项
-
反过来,再删除/插入空值匹配行
这就对应后面的核心算法:两阶段增量更新。
❷ 规律二:
阶段二的增量,总是由阶段一中某些列填充 null 得到。
有了这两条规律,你内心可能已经有了初步的求解思路:我们可不可以先通过算出阶段一的增量,再填充空值,得到阶段二的增量?
下一节,我们完整地求解这个增量更新问题。
问题求解
上一节的例子很简单。但是,当表的数量越来越多,连接方式多种多样(left, right, full),口算就很困难了,我们需要维护一些额外的数据结构,帮助我们快速确定需要删除或者填充哪些行,以保证视图和基表变更的一致。
为了求解空值填充的问题,我们需要在基表和物化视图之间,引入辅助的中间层:增量维护图。
这里需要耐心地走完以下五个步骤:
-
解析 query,分析可能的 tuple 类型
-
构建增量维护图
-
更新增量维护图
-
计算主增量
-
计算次增量
step1 分类(找点)
我们先解析 query,把所有可能的结果做分类。
如果用 1 表示 join 的时候非空,0 表示空值填充,那么查询结果会包含哪些类型?
我们只需要一一枚举。
从基础的两个表开始,到三个表:
扩展到六个表:
现在,已经对所有可能产生的结果进行了枚举分类。
step2 建图(连边)
如果把每个类看作一个点,再去分析点和点之间的关系,我们又可以构建成一张图,管它叫“增量维护图”,也就是我们需要的中间层。
具体而言:
-
点表示:若干表的连接组合
-
边表示:点之间的包含关系
step3 更新图
我们还可以进一步对图节点状态做分类。
根据某个点是否受更新基表的影响,可以分为:
-
直接影响(标记黄色)
- 包含当前被修改的基表T
-
间接影响(标记绿色)
- 不包含T,但是有直接影响的父节点
-
无影响(标记灰色)
- 不包含T,且无直接影响的父节点
我们给这些节点产生的增量命个名:
直接包含修改基表的点,产生的叫主增量。间接受影响的点,产生的增量叫次增量。
现在,我们的问题变成了如何求解这两类增量。
step4 计算主增量
step5 计算次增量
这两步我们通过具体的例子来看:
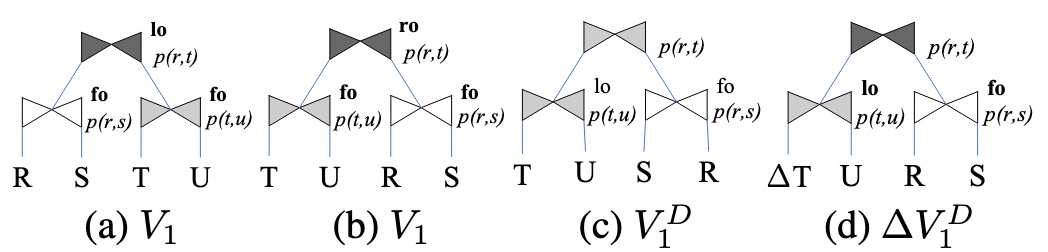
我们分析一下这张图:
-
假设我们在基表S上删除了红色的这一行。
-
那么物化视图上也要删除掉这行和其它表join的结果,就是主增量。
-
根据这条主增量,我们又可以在图里找到它对应的孩子节点,进而算出绿色的这两行次增量。其实,它们就是因为连接的时候不匹配而产生的空值填充行。
经过这两个“有主有次”的过程,我们的两阶段更新就完成了。
看到这里,你可能对主增量和次增量有个大概的了解,但具体的计算规则还比较模糊,我们在下一节详细展开。
两阶段增量计算
我们回顾下之前提到的框架:
主增量的计算
后面会省略一些公式的推导和正确性证明,直接给出结论。
感兴趣的同学可以前往论文或者技术报告看证明过程。
https://www.microsoft.com/en-us/research/wp-content/uploads/2005/06/tr-2005-78.pdf
主增量算法描述
输入:mv 的定义query
输出:mv 的主增量$\Delta mv$
计算公式:在 query 定义公式中,经过两个步骤:
-
用基表T的修改$\Delta T$替换T
-
再对连接树进行 join 类型的改写,得到的结果为主增量。
可能的疑问
看完前面的例子,你可能会觉得主增量计算和原框架 inner join 有点像,甚至猜测:
主增量是不是基表增量和其它表 inner join 得到的结果?
答案是否定的,还可能是 left join 或者 right join。
为什么呢?我们重新思考下主增量的实际含义:直接包含当前被修改的基表 T,因为 T 的变化$\Delta T$,而产生的增量叫主增量。那么只要 T 的位置非空,换成非空的$\Delta T$,就是我们需要的主增量。
具体而言:
-
在 inner join 中,T 一定非空;
-
在 left join 中,如果 T 在左侧,它也是非空的,也要保留;
-
同理,在 right join 中,如果 T 在右侧,那么也会产生主增量。
-
但对于 full join,就需要改写成 left join(T 在左侧)或者 right join(T 在右侧)。
示例
我们根据视图的定义:
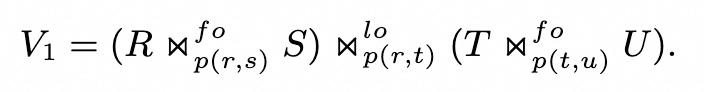
-
直接将对基表T的变更记为$\Delta T$,再进行一些剪枝
- 细心的人可能发现这里对 join order 进行了改写,T 被等价地移到最左侧。这里其实是一种性能优化。因为基表的增量一般比较小,放左边可以构成一颗左深树。
-
改写
-
替换后,需要进行一定的逻辑等价改写,最终得到主增量:
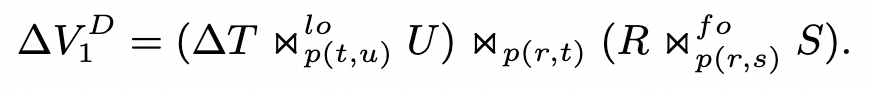
-
具体的替换规则(略)
- 假设 T 在左侧,从 T 开始向根节点方向走
-
将 full join改为left join
- 将right join改为inner join
次增量的计算
次增量的计算公式比较复杂,我们后面举直观的例子大概理解下就行。
涉及到次增量的流程包括三层(query -> graph -> secondary_delta):
-
根据 query 计算得到维护图
-
根据基表的变更,更新维护图状态
-
根据维护图和主增量,生成次增量
具体而言,基表T发生的变更可能有插入和删除两种情况,下面分类讨论:
一、插入操作
论文中次增量的公式如下:
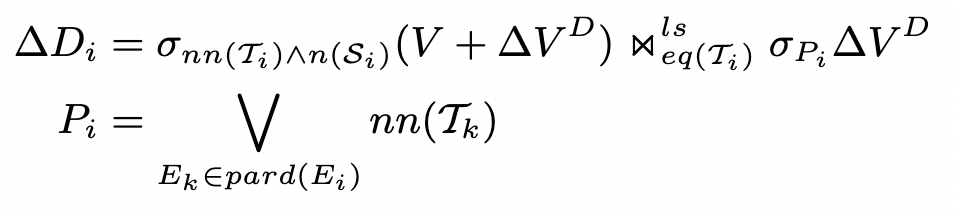
公式太绕了🙅,我们从增量维护图中截取一小块,用例子直观理解一下:
二、删除操作
- 论文中次增量的公式如下:
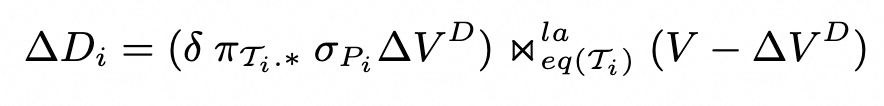
还是绕过公式,直接看例子:
三、扩展到多Term
当基表发生变更时,一个Term可能同时会受多个parent Term的影响,因此需要把所有的影响都计算出来,最后应用到物化视图。(当然实现中也就是多一重for循环的事了)
到这里可能还会有个疑问,影响次增量的一定是直接父节点吗?父节点的父节点(爷爷)算吗?
答案是:算。
从前面的例子可以看出:
点 RST 是 R 的间接父节点(也就是爷爷),那么它的主增量,同样也会产生 R 点上的次增量。
总结展望
本文主要介绍了
-
增量物化视图的背景、需求
-
PolarDB PG 当前增量更新框架的原理
-
增量更新支持 outer join 的原理
后续优化思路
针对 outer join 的性能优化
优化的思路主要有:
-
主增量计算的左深树优化
-
改 join order 和 join type,把数据量小的基表增量放左侧
-
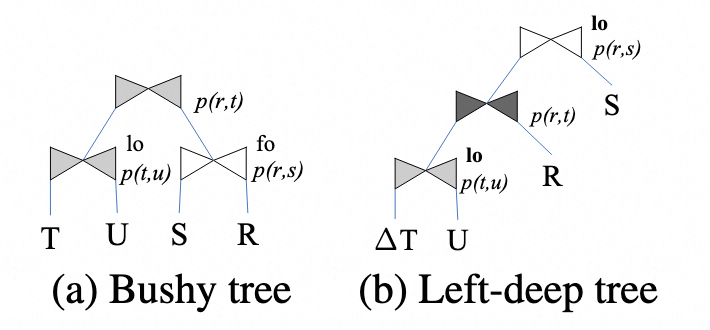
-
-
图的剪枝
-
左外连接优化
- 具体可以参考ADB的论文:https://www.vldb.org/pvldb/vol18/p5153-zhou.pdf
-
外键约束
- 外键约束可以帮助我们排除掉一些不会存在的空值语义
-
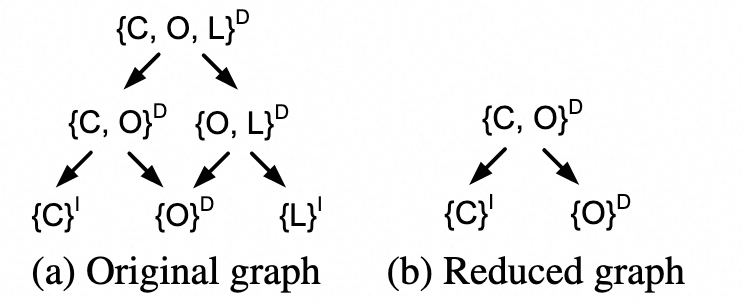
-
简化查询执行
- 主增量和次增量的合并
outer join 的功能扩展
目前支持的 outer join 功能在与其它功能混用时需要进行适配工作,例如:
-
outer join + distinct
-
outer join + agg
-
outer join + 物化视图的级联嵌套等